Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 50
Uma bola de argila de é arremessada horizontalmente, com velocidade de , contra um bloco de em repouso sobre uma superfície livre de atrito. Ela bate no bloco e fica grudada. A argila exerce uma força constante sobre o bloco durante os decorridos para a argila atingir o repouso relativo ao bloco. Após , o bloco e a argila estão deslizando sobre a superfície, formando um único corpo.
a. Qual é o valor da velocidade após a colisão?
b. Qual é a força que a argila exerce sobre o bloco durante a colisão?
c. Quanto vale a força do bloco sobre a argila?
NOTA Este problema pode ser tratado usando-se as leis de conservação que você aprenderá nos próximos capítulos. Todavia, aqui se pede que você resolva os problemas com o emprego das leis de Newton.
Passo 1
Como foi dito no enunciado, devemos resolver o exercício pela 3ª Lei de Newton. Vamos anotar foi dado da argila
E o bloco
E o tempo de colisão é de
Anotando os dados importantes, faremos um esqueminha o movimento da argila atingindo o bloco
O exercício pede para descobrirmos a velocidade final em (a). Em (b) pede a força da argila durante a colisão e em (c) do bloco em relação a argila
Passo 2
Em (a) temos que descobrir a velocidade final dos blocos.
As forças são conservativas, pois o bloco e a argila se juntaram após a colisão, e que é um par ação e reação, assim, terão sentidos contrários, vamos considerar a argila negativa
Isolado
Tá, mas e a velocidade, como que chega nela? Vamos ter que isolar a velocidade da argila e do bloco, já os dois depois da colisão de movem juntos e com a mesma velocidade
Se usarmos a equação do movimento
E substituímos em relação a argila
Substituindo para o bloco e que a velocidade inicial é zero
Substituindo as equações e em nas velocidades iguais dita em
Vamos deixar em função de
Depois de tanta conta, podemos isolar as funções das acelerações que encontramos em e !
Substituindo
Encontrada a aceleração do bloco, podemos voltar em para encontrar a velocidade da argila
E como as velocidades depois da colisão é igual para o bloco e argila, chegamos à conclusão que a velocidade do movimento é de 10 m/s! Ufa! O exercício é longo, mas não podemos desanimar! Ainda tem b e c pra responder, bora lá!
Passo 3
(b) O exercício pede a força da argila exercida pelo bloco, fazendo um esqueminha das forças
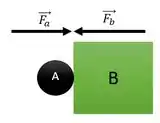
Assim, a força exercida de A em B, é a própria força de B! Em número quer dizer
A força é de 90 N!
Passo 4
(b) O mesmo raciocínio se repete para a força exercida pelo bloco sobre a argila, ou seja, encontramos , só temos um probleminha, temos que descobrir a aceleração de A, para isso, vamos usar a equação (v) que encontramos no item a
O negativo é o sentido da aceleração, usando a força
Aeee!
Resposta
a.
b. 90 N
c. -90 N