Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 40
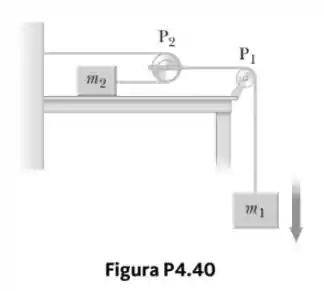
Um corpo de massa está pendurado por uma corda que passa sobre uma polia fixa muito leve como mostrado na Figura P4.40. A corda conecta-se a uma segunda polia muito leve . Uma segunda corda passa em torno dessa polia com uma extremidade presa a uma parede e a outra ponta a um corpo de massa sobre uma mesa horizontal, sem atrito.
- Se e são, respectivamente, as acelerações de e , qual a relação entre essas acelerações?
- Encontre expressões para as tensões nas cordas e
- as acelerações e em termos das massas , e .
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
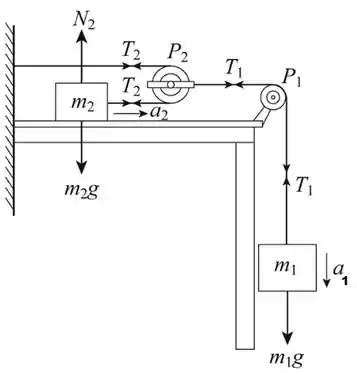
Vamos começar com um diagrama para facilitar:
Passo 2
Letra a:
De acordo com o diagrama temos:
Então, derivando:
Passo 3
Letra b:
Aplicando a segunda lei de Newton à massa na direção vertical assumindo que para baixo é positivo:
E,
Então, substituindo:
Passo 4
Letra c:
Para achar as acelerações, temos:
Resposta
Exercícios de Livros Relacionados
Determine a aceleração de cada bloco da Figura 5.71 em função de m 1 , de m 2 e de g . Não existe nenhum atrito em nenhuma parte do sistema.
No sistema da figura, m 1 = 1K g ,m 2 = 3 K gem 3 = 2K g , e as massas das polias e das cordas são desprezíveis. Calcule as acelerações a 1 ,a 2ea 3 das massas m 1 ,m 2em 3 , e a tensão T da corda.
Para a situação da FIGURA PD7.51, obtenha uma expressão para a aceleração de m 1 . Considere a mesa desprovida de atrito.Sugestão: reflita cuidadosamente sobre o vínculo de aceleração.
Quanto vale a aceleração do bloco de 2,0 kg sobre a mesa livre de atrito da FIGURA PD7.52?Sugestão: reflita cuidadosamente sobre o vínculo de aceleração.
43. Os centenários elevadores de Valparaíso, no Chile, são pequenos bondes que sobem e descem as ruas inclinadas. Como mostra a FIGURA P7.43, um elevador sobe enquanto outro desce. Os vagões usam um a