Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 39

Quatro fios longos, retilíneos e paralelos, conduzem corrente I. Em um plano perpendicular aos fios, eles estão nos vértices de um quadrado de lado a. Determine a magnitude da força por unidade de comprimento em um dos fios se:

a) Todas as correntes estão no mesmo sentido.

b) As correntes nos fios em vértices adjacentes têm sentidos opostos.

Passo 1

a)

Meus grandes gênios!

Vamos considerar que o campo magnético resultante é dado por:

B → = B 1 → + B 2 → + B 3 →

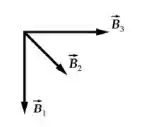
Portanto:

B 1 → = - μ 0 4 π 2 I a ∙ j

B 2 → = μ 0 4 π 2 I a 2 ∙ cos ⁡ 45 ° ∙ i - j = μ 0 4 π 2 I 2 a ∙ ( i - j )

B 3 → = μ 0 4 π 2 I a ∙ i

Com isso:

B → = B 1 → + B 2 → + B 3 → = - μ 0 4 π 2 I a ∙ j + μ 0 4 π 2 I 2 a ∙ ( i - j ) + μ 0 4 π 2 I a ∙ i

Resolvendo, encontraremos:

B → = 3 μ 0 4 π I a i - j

Sabendo que:

F l = B I

Então

F → l = 3 μ 0 4 π I a ∙ I i - j

F → l = 3 μ 0 4 π I 2 a i - j

Porém, queremos saber o módulo do vetor, logo:

F l = 3 μ 0 4 π I 2 a 2 + 3 μ 0 4 π I 2 a 2

F l = 3 2 μ 0 4 π I 2 a

Passo 2

b)

A letra b) tem resolução parecida com a letra a)!

Vamos considerar que o campo magnético resultante é dado por:

B → = B 1 → + B 2 → + B 3 →

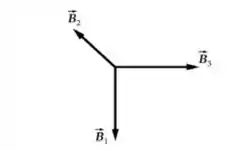
Portanto:

B 1 → = - μ 0 4 π 2 I a ∙ j

B 2 → = μ 0 4 π 2 I a 2 ∙ cos ⁡ 45 ° ∙ - i + j = μ 0 4 π 2 I 2 a ∙ ( - i + j )

B 3 → = μ 0 4 π 2 I a ∙ i

Com isso:

B → = B 1 → + B 2 → + B 3 → = - μ 0 4 π 2 I a ∙ j + μ 0 4 π 2 I 2 a ∙ ( - i + j ) + μ 0 4 π 2 I a ∙ i

Resolvendo, encontraremos:

B → = μ 0 4 π I a i - j

Sabendo que:

F l = B I

Então

F → l = μ 0 4 π I a ∙ I i - j

F → l = μ 0 4 π I 2 a i - j

Porém, queremos saber o módulo do vetor, logo:

F l = μ 0 4 π I 2 a 2 + μ 0 4 π I 2 a 2

F l = 2 μ 0 4 π I 2 a

Resposta

a )   F l = 3 2 μ 0 4 π I 2 a

b )   F l = 2 μ 0 4 π I 2 a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O fio mostrado na Fig.31-31 transporta uma corrente i. Que campo magnético B é produzido no centro C do semicírculo (a) por cada segmento retilíneo de comprimento L, (b) pelo segmento semicircular de
Dispõe-se de um fio de comprimento L, onde podemos estabelecer uma corrente i. O fio pode ser dobrado na forma de um círculo ou de um quadrado. Mostre que o quadrado dará o maior valor para B no ponto
Um fio transportando uma corrente i tem a configuração mostrada na Fig. 31-35. Dois trechos retilíneos semi-infinitos, ambos tangentes ao mesmo círculo, estão ligados por um arco circular de ângulo ce
Mostre que o módulo do campo magnético produzido no centro de uma espira retangular de fio de comprimento L e largura W transportando uma corrente i é B = 2 μ 0 i π L 2 + W 2 1 / 2 L W Mostre que, par
Determine o campo magnético B no ponto P da Fig. 31 -40 (veja o Problema 23).