Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 112

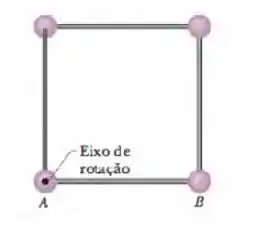
Quatro partículas, todas de massa m = 0,2 k g , ocupam os vértices de um quadrado com l = 0,5 m de lado. As partículas estão ligadas por uma barra de massa desprezível. Este corpo rígido pode girar em um plano vetical em torno de um eixo horizontal. A que passa por uma das partículas. O corpo é liberado a partir do repouso com a barra A B na horizontal, como mostra a figura abaixo.

( a ) Qual é o momento de inércia do corpoem relação ao eixo A ?

( b ) Qual é a velocidade angular do corpo em relação ao eixo A no instante em que a barra A B passa pela posição vertical?

Passo 1

Olá pessoal, tudo bem? Vamos praticar o cálculo de momento de inércia e dinâmica rotacional?

O problema pede o momento de inércia em relação ao eixo A , então temos que analisar a distância perpendicular das massas até o eixo de rotação.

Como uma das massas está no eixo de rotação, essa não contabiliza para o momento de inércia. Duas delas estão a uma distância r = l = 0,5 m e a outra está na diagonal do quadrado e essa distância vale r = l 2 .

Outra coisa, as barras são de massa desprezível, então elas também não contam no cálculo de I .

Ok? Agora podemos passar para o cálculo de I :

I = m r 2 = 2 . m l 2 + m l 2   2

I = 4 m l 4 = 4.0,2 . 0,5 2 = 0,2 k g m ²

Passo 2

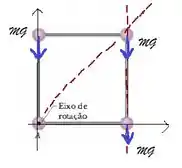Agora o problema quer a velocidade angular. Pra entender melhor o que está contecendo eu fiz um desenho pra você:

Assim que o sistema é liberado do repouso, a força gravitacional que está agindo em cada massa faz com que o sistema gire, em torno do eixo de rotação, em sentido horário.

A força gravitacional está assinalada em cada massa no desenho. Como podemos ver apenas duas das três forças fazem torque sobre o sistema, ocasionando na rotação.

Daí você se pergunta: mas por que isso? Eu respondo: o eixo vertical não coincide com a direção da força peso aplicada em uma das massas ali em cima? Sim! Então o braço de alavanca é zero, logo o torque é nulo!

Para as outras massas temos torques não nulos. Pela segunda lei de Newton para rotações temos:

τ → r e s = I . α → r e s

m g . l s e n 90 ° + m g . l 2 s e n 135 ° = I . α

m g l + 2 2 2 m g = I α

2 m g l I = α = 2.0,2.9,8.0,5 0,2 = 9,8 r a d / s ²

Agora que sabemos a aceleração angular, podemos determinar a velocidade angular ω . Sabendo que a variação angular foi de π / 2 , pelas equações de movimento rotacional temos:

ω 2 = ω 0 2 + 2 α ( Δ θ )

ω 2 = 0 + 2.9,8 . π 2

ω = 5,54 r a d / s

É isso! Vamos pra próxima?

Resposta

( a ) 0,2 k g m ²  

b 5,54 r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de massa m 1=2,00k g e outro de massa m 2=6,00k g são conectados por um fio sem massa sobre uma roldana em forma de disco sólido de raio R=0,250m e massa M=10,0k g . A rampa fixa, em formato
Um cordão é amarrado ao redor de um disco uniforme de raio R e massa M . O disco é solto do repouso com o cordão vertical e sua ponta de cima amarrada a uma barra fixa (Fig. P10.78). Mostre que a tens
Uma barra uniforme longa de comprimento L e massa M é centrada em um pino horizontal sem atrito por uma extremidade. A barra é liberada do repouso em uma posição vertical como mostrado na Figura P10.6
Uma demonstração comum, ilustrada na Figura P10.76, consiste em uma bola repousando em uma extremidade de uma mesa uniforme de comprimento l que é presa na outra extremidade e elevada a um ângulo de θ
Suponha que uma pessoa se incline para a frente para levantar um peso “com suas costas”, como mostrado na Figura P10.79a. A coluna vertebral gira principalmente na quinta vértebra lombar com a força d