Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.4 - Ex. 8
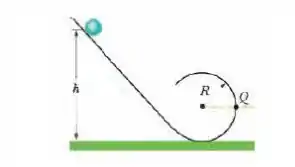
Na figura abaixo, uma bola maciça de latão de massa rola suavemente ao longo do trilho quando é liberada a partir do repouso no trecho retilíneo. A parte circular do trilho tem um raio e a bola tem um raio .
Quanto vale se a bola está na iminência de perder contato com o trilho quando chegar ao ponto mais alto da parte curva do trilho?
Se a bola é liberada a uma altura , qual é
o módulo e
a orientação da componente horizontal da força que age sobre a bola no ponto ?
Passo 1
Olá pessoal, tudo bem? Vamos praticar um pouco de mecânica rotacional?
O sistema é conservativo, ou seja, não tem forças que fazem o sistema dissipar energia, então podemos comparar a soma das energias em dois pontos. Vou comparar o ponto em qua a bolinha está na altura , pois ali não tem energia cinética, apenas a potencial gravitacional. O segundo ponto é no alto do trilho circular, pois é ali que a bola pode se descolar dos trilhos.
Então a soma das energias de cada ponto tem que ser igual:
Mas aqui vai o pulo do gato de das questões de energia envolvendo rotações: a questão do deslizamento! Se não há deslizamento (como é nosso caso) a velocdade angular é . Daí conseguimos colocar toda energia cinética em termos da velocidade do centro de massa.
Ta, mas e aquele ? É o momento de inércia de uma esfera maciça!
Vamos substituir tudo?
Juntando os semelhantes e cortando as massas:
Agora tu te pergunta da onde eu vou tirar a velocidade né? Bom, nesse instante, na iminência de descolar dos trilhos, é quando a força normal é zero, e a força centrípeta é igual ao peso do objeto. Sendo assim:
Pronto, agora é só substituir!
Cortando em todos os termos:
Passo 2
Agora o problema fornece uma altura inicial e pede o módulo da força resultante no ponto . Vou usar do mesmo princípio de conservação de energia, mas agora entre os pontos de altura inicial () e o ponto :
Podemos cortar as massas:
Mas por que determinar a velocidade? Bom, lembra que a força horizontal que age na partícula é a força normal N e ela é igual à força centrípeta (que varia com a velocidade ao quadrado!)? Então:
Logo:
Passo 3
Já quando a bola passa pelo ponto , a sua componente horizontal possui direção radial ao centro do loop.