Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 72

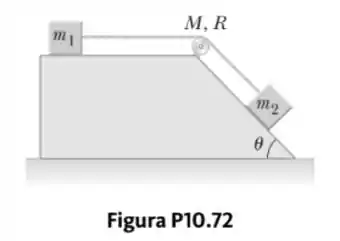
Um bloco de massa m 1   =   2,00   k g e outro de massa m 2   =   6,00   k g são conectados por um fio sem massa sobre uma roldana em forma de disco sólido de raio R   =   0,250   m e massa M   =   10,0   k g . A rampa fixa, em formato triangular, forma um ângulo de θ   =   30,0 ° como mostrado na Figura P10.72. O coeficiente de atrito cinético é 0,360 para ambos os blocos.

  1. Desenhe diagramas de forças dos dois blocos e da roldana.
  2. Determine a aceleração dos dois blocos e
  3. as tensões no fio nos dois lados da roldana.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Os diagramas são:

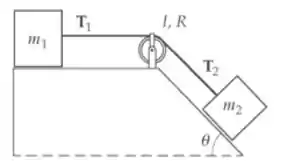
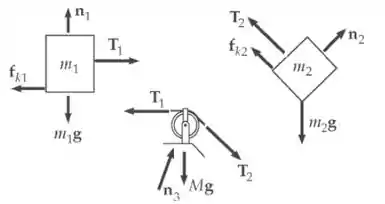
A partir das figuras, temos:

Para m 1 :

∑ F y = m a y   n o s   d á :   + n - m 1 g = 0 n 1 = m 1 g

Com   f k 1 = μ k n 1 .

∑ F x = m a x   n o s   d á :   - f k 1 + T 1 = m 1 a                   ( 1 )

Para a polia, ∑ τ = I α nos dá:

- T 1 R + T 2 R = 1 2 M R 2 a R

- T 1 + T 2 = 1 2 M R a R → - T 1 + T 2 = 1 2 m a                   ( 2 )

Para m 2 :

+ n 2 - m 2 g c o s ⁡ θ = 0 → n 2 = m 2 g c o s ⁡ θ f k 2 = μ k n 2 - f k 2 - T 2 + m 2 gsin ⁡ θ = m 2 a                 ( 3 )

Passo 2

Letra b:

Adicione as equações [1], [2] e [3] e substitua as expressões para f k 1   e  n 1 ,   e   - f k 2   e   n 2 :

- f k 1 + T 1 + - T 1 + T 2 - f k 2 - T 2 + m 2 g s i n ⁡ θ = m 1 a + 1 2 M a + m 2 a - f k 1 - f k 2 + m 2 g s i n ⁡ θ = m 1 + m 2 + 1 2 M a

- μ k m 1 g - μ k m 2 g c o s ⁡ θ + m 2 g s i n ⁡ θ = m 1 + m 2 + 1 2 M a a = m 2 sin ⁡ θ - μ k cos ⁡ θ - μ k m 1 m 1 + m 2 + 1 2 M g

a = 6.00 k g sin ⁡ 30.0 ∘ - 0.360 cos ⁡ 30.0 ∘ - 0.360 2.00 k g 2.00 k g + 6.00 k g + 1 2 10.0 k g g a = 0.309 m / s 2

Passo 3

Letra c:

Da equação [1]:

- f k 1 + T 1 = m 1 a → T 1 = 2.00 k g 0.309 m s 2 + 7.06 N = 7.67 N

Da equação [2]:

- T 1 + T 2 = 1 2 M a → T 2 = 7.67 N + 5.00 k g 0.309 m s 2 = 9.22 N

Resposta

  1. Ver diagramas
  2. 0.309 m / s 2
  3. 7.67 N   e   9.22 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura o bloco 1 tem massa m1 = 460 g , o bloco 2 tem massa 500 g , e a polia ,que está montada em um eixo horizontal com atrito desprezível , tem um raio R = 5 cm.Quando o sistema é liberado a par
Na figura abaixo, um cilindro com uma massa de 2,0 Kg pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1=6,0 N, F → 2=4,0 N, F → 3=2,0 N e
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2
Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Na figura abaixo, mostra um disco homogêneo que pode girar em torno do centro como um carrossel. O disco tem um raio de 2,00 cm e uma massa de 20,0 g e está inicialmente em repouso. A partir do instan