Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Serway e Jewett - Física para cientistas e engenheiros - Vol1 - Ed: 1º - Capítulo 10.Problemas - Ex. 73a

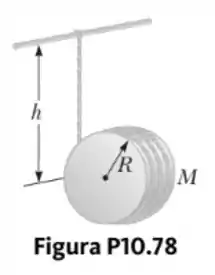
Um cordão é amarrado ao redor de um disco uniforme de raio R e massa M . O disco é solto do repouso com o cordão vertical e sua ponta de cima amarrada a uma barra fixa (Fig. P10.78). Mostre que

  1. a tensão no cordão é um terço do peso do disco,
  2. o módulo da aceleração do centro de massa é 2 g / 3 , e
  3. a velocidade do centro de massa é 4 g h 3 1 / 2   após o disco ter descido uma distância h .
  4. Verifique sua resposta para a parte (c) usando a abordagem de energia.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Em y, ∑ F y = m a y :

∑ F = M g - T M = a

a = M g - T M

Como ∑ τ = I α , então:

∑ τ = T R = I α = 1 2 M R 2 a R

a = 2 T M

Passo 2

Letra a:

M g - T M = 2 T M

T = M g 3

Passo 3

Letra b:

a = 2 T M = 2 M g 3 M

a = 2 3 g

Passo 4

Letra c:

Como v i = 0   e   a = 2 3 g ,

v f 2 = v i 2 + 2 a h nos dá:

v f 2 = 0 + 2 2 3 g h

v f = 4 g h 3

Passo 5

Letra d:

Agora verificamos esta resposta. Exigindo a conservação da energia mecânica para o sistema disco-Terra, temos:

U i + K rot  , i + K trans  , i = U f + K rot  , f + K trans  , f m g h + 0 + 0 = 0 + 1 2 I ω 2 + 1 2 m v 2 m g h = 1 2 1 2 M R 2 ω 2 + 1 2 M v 2

Quando não há deslizamento, ω = v R   e   v = 4 g h 3

Então, a resposta é a mesma.

Resposta

  1. M g 3
  2. 2 3 g
  3. 4 g h 3
  4. Então, a resposta é a mesma.

Exercícios de Livros Relacionados

Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Na figura (a) abaixo, uma placa de plástico de forma irregular, com espessura e massa específica (massa por unidade de volume) uniformes, gira em torno de um eixo perpendicular à face da placa passand
Na figura abaixo, mostra as partículas 1 e 2, ambas de massa m, presas às extremidades de uma barra rígida de massa desprezível e comprimento L1 + L2, com L1=20 cm L2= 80 cm. A barra é mantida horizon
Na figura abaixo, mostra as partículas 1 e 2, ambas de massa m, presas às extremidades de uma barra rígida de massa desprezível e comprimento L1 + L2, com L1=20 cm L2= 80 cm. A barra é mantida horizon
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo