Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 41
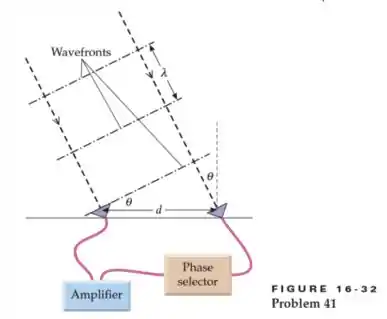
Um radiotelescópio astronômico consiste em duas antenas separadas por uma distância de 200 m. Ambas as antenas são sintonizadas na frequência de 20 MHz. Os sinais de cada antena são alimentados em um amplificador comum, mas um sinal passa primeiro por um seletor de fase que atrasa sua fase em uma quantidade escolhida, para que o telescópio possa "olhar" em diferentes direções (Figura 16-32). Quando o atraso de fase é zero, as ondas de rádio planas que são incidentes verticalmente nas antenas produzem sinais que adicionam construtivamente ao amplificador. Qual deve ser o atraso de fase para que os sinais vindos de um ângulo θ = 10° com a vertical (no plano formado pela vertical e a linha que une as antenas) sejam construtivamente adicionados no amplificador? Dica: as ondas de rádio viajam a .
Passo 1
Bom, como podemos ver pelo desenho, a distância a mais que a onda da direita irá percorrer em relação à da direita corresponde ao cateto de um triangulo retângulo, vamos chamar essa diferença entre as duas distancias percorridas de , como ele é oposto a podemos escrever uma relação usando o seno desse ângulo:
Isolando
Passo 2
Essa distancia a mais causará um atraso entre os sinais das antenas, podemos expressar essa fase através da equação:
Passo 3
Como o enunciado nos dá a velocidade da onda de rádio e a frequência das antenas, podemos escrever em termos das duas grandezas pela equação da velocidade da onda:
Isolando :
Substituindo e na equação do Passo 2:
Colocando os valores numéricos: