64. Na Equação , considere o caso . Faça um desenho e mostre que esse caso se reduz à situação de uma única fenda com largura . A seguir, mostre que a Equação se transforma na Equação para uma única fenda com largura .
Passo 1
Então nesse problema só temos que pegar a equação e substituir e ir mexendo para chegar em .
O desenho que o enunciado pede não é nada demais é só o seguinte:
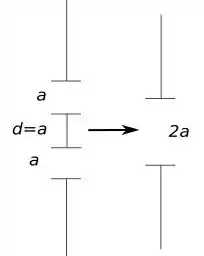
Passo 2
Agora vamos mexer com a equação , dada por:
Sendo que
Precisamos de apenas mais uma informação, que é:
Como estamos analisando o caso que , então temos que
Assim a equação fica da seguinte forma:
Agora vamos usar uma identidade trigonométrica para conseguirmos simplificar essa expressão, temos:
Então nossa equação fica da seguinte forma:
Agora vamos fazer uma substituição, vamos chamar , assim:
Onde é a largura a fenda.
Então temos que:
Que é a equação para uma fenda única de largura .
Resposta
Ei, a resposta está no passo a passo :)