Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 74
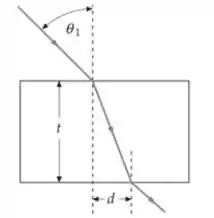
Luz incide em uma lâmina de material transparente a um ângulo , como mostrado na Figura 31-60. A lâmina tem uma espessura e um índice de refração . Mostre que , onde é a distância mostrada na figura.
Passo 1
Falaaa meu caro, tudo certinho?
Vamos entender o que esse maluco ta dizendo: precisamos provar que usando a figura dada pelo exercício, certo?
Aqui podemos aplicar a lei de Snell na interface de placa de ar para expressar o índice de refração em termos de e e, em seguida, usar a geometria da figura para relacionar com e .
Aplicar a lei de Snell à primeira interface produz:
Do diagrama:
Substitua para obter:
Resposta
Exercícios de Livros Relacionados
A luz passa por três blocos paralelos de espessuras e índices de refração diferentes. A luz incide no primeiro bloco e, finalmente, refrata para dentro do terceiro bloco. Mostre que o bloco do meio nã
Em um laboratório de física, a luz de comprimento de onda igual a 490n m atravessa o ar de um laser até uma fotocélula em 17,0n s . Quando um bloco de vidro de 0,840m de espessura é colocado sob o fei
Um raio de luz proveniente do ar incide sobre um bloco de um material sólido transparente cujo indice de refração é n . Sabendo que n = 1,38 , qual deve ser o maior ângulo de incidência θ a para que o
A luz que atravessa um material de indice de refração n 1 incide com um ângulo θ 1 , em relação à normal sobre a interface com um bloco de material que possui lados paralelos e índice de refração n 2
Uma placa de vidro com espessura de 2.50m m e um índice de refração de 1,40 é colocada entre uma tela e uma fonte de luz puntiforme de comprimento de onda igual a 540n m (no vácuo). A distância entre