Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 80

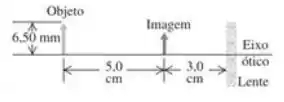
A figura abaixo mostra um objeto e sua imagem formada por uma lente delgada. (a) Qual é a distância focal da lente, e qual é o tipo de lente (convergente ou divergente)? (b) Qual é a altura da imagem? Ela é real ou virtual?

Passo 1

(a) Pra calcular a distância focal da lente, vamos usar essa fórmula aqui:

1 s + 1 s ' = 1 f

A distância s da lente até o objeto é s = 5,0 + 3,0 = 8,0   c m e a distância s ' da imagem até a lente é s ' = - 3,0   c m .

O sinal negativo de s ' aparece porque a imagem está na frente do espelho (do mesmo lado do objeto).

Então:

1 f = 1 s + 1 s ' = s + s ' s s '

f = s s ' s + s '

f = 8,0 - 3,0 8,0 - 3,0 = - 4,80   c m

O fato de que a distância focal é negativa indica que a lente é divergente.

Passo 2

(b) Se você quer encontrar a altura da imagem, primeiro precisa calcular a ampliação m :

m = - s ' s = - - 3,0 8,0

m = 0,375

E então a altura da imagem é:

y ' = m y

y ' = 0,375 6,50   m m

y ' = 2,44   m m

Como a imagem se forma na frente do espelho ( s ' < 0 ), ela é virtual.

Resposta

(a) A distância focal é f = - 4,80   c m e a lente é divergente.

(b) A altura da imagem é 2,4 4   m m e ela é virtual.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Demonstre que a distância focal de uma lente delgada biconvexa pode ser expressa em função do diâmetro D da lente, de sua espessura t e do seu índice de refração n 12 relativo ao meio.
Se dermos um pequeno deslocamento Δ p à posição de um objeto, ao longo do eixo de uma lente delgada, a imagem desse objeto se desloca de Δ q . A razão Δ q / Δ p chama-se aumento longitudinal. Demonstr
Chama-se potência P de uma lente, o inverso de sua distância focal f (se f for medida em m , P se mede em d i o p t r i a s ). Considere duas lentes delgadas de potências P 1 e P 2 em contato uma com
Uma lente delgada biconvexa tem distância focal f .a) Demonstre que a distância mínima entre um objeto e sua imagem real é igual a 4 f . Para que distância p do objeto à lente esse mínimo é atingido?
A Figura 34.56 mostra uma planta perto de uma lente delgada. O raio mostrado é um dos principais raios da lente. Cada quadrado tem 2,0 cm na direção horizontal, mas na direção vertical a escala é dife