Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 86
Uma barra transparente com de comprimento e índice de refração de é cortada formando um plano na extremidade direita e uma superfície hemisférica com um raio de na extremidade esquerda. Um objeto é colocado à esquerda do vértice da superfície hemisférica. (a) Qual é a posição da imagem final? (b) Qual é a ampliação?
Passo 1
(a) Já que estamos passando de um material para o outro (ar e interior da barra), temos que usar essa fórmula aqui:
Primeiro, o objeto é colocado a da parte hemisférica.
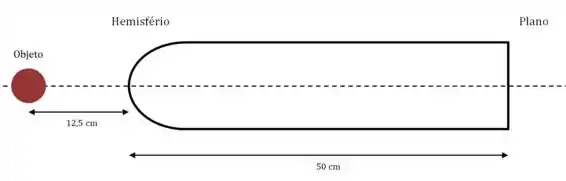
Onde essa primeira imagem é formada?
Então a imagem é formada lá atrás:
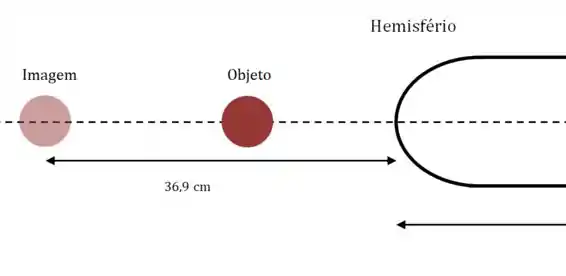
Passo 2
A distância dessa imagem até a superfície plana que fica do lado direito é:
Então:
Na superfície plana, temos , então a fração do lado direito tende a zero:
Passo 3
A fórmula para a ampliação é:
Então, para o primeiro processo:
E no segundo:
E pra achar a ampliação final, é só multiplicar essas duas ampliações:
Resposta
(a) A posição da imagem final é . Ou seja, à esquerda do vértice do hemisfério.
(b) A ampliação final é .