Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 89
A rapidez da cabeça de um pica-pau de cabeça vermelha atinge antes do impacto contra a árvore. Se a massa da cabeça é e a força média na cabeça é , encontre (a) a aceleração da cabeça (suposta constante), (b) a profundidade de penetração na árvore, e (c) o tempo que a cabeça leva para parar.
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão.
A ideia é a gente imaginar que a cabeça do pica-pau é um objeto com uma velocidade inicial que vai adquirir desaceleração constante ao chegar na árvore (a árvore desacelera a cabeça dele equanto ele tenta penetra-la), uma força resultante e massa .
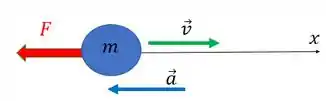
Então, a gente pode usar a equação da segunda lei de Newton para achar a aceleração desse objeto como ele pede:
A aceleração será:
Substituindo os valores, temos:
Ela é negativa exatamente por se opor ao movimento que tem sentido positivo .
Passo 2
b) Cara, aqui ele quer saber o quanto esse objeto (a cabeça do pica pau) conseguiu andar até ser parada totalmente pela árvore.
Basicamente, temos um objeto com desaceleração constante e a gente quer saber o deslocamento dele , se sabemos a velocidade inicial e a velocidade final .
Podemos usar torricelli pois essa expressão relaciona os dados que a gente sabe e o que a gente quer descobrir:
Isolando o que queremos:
Como a velocidade final é nula, temos que:
Substituindo os valores, temos:
Passo 3
c) Agora a gente quer saber o tempo decorrido nesse movimento do item anterior. Podemos usar a definição de aceleração:
Isolando quem a gente quer
Como a velocidade final é nula, temos que:
Substituindo os valores, temos:
Prontinho, acabamos! Ficamos diferente do gabarito, mas é porque há um errinho no gabarito deles mesmo, ele consideram , mas o enunciado diz que é .
E vou dizer ein, essa questão foi bem criativa haha
