Um professor de colégio sugeriu, certa vez, o seguinte método para medir a magnitude da aceleração de queda livre: pendure uma massa em um fio bem fino (comprimento ) para fazer um pêndulo com a massa a uma altura do chão, quando a massa estiver em seu ponto mais baixo . Puxe o pêndulo até que o fio forme um ângulo com a vertical. Bem acima do ponto , coloque uma lâmina de barbear posicionada de modo a cortar o fio quando uma lâmina de barbear posicionada de modo a cortar o fio quando a massa passar pelo ponto P. Quando o fio é cortado, a massa é projetada horizontalmente e atinge o solo a uma distância horizontal do ponto . A idéia era que a medida de , como função de , deveria de alguma maneira determinar . Fora algumas óbvias dificuldades experimentais, o experimento tinha uma falha fatal: não depende de ! Mostre que isto é verdade e que depende apenas do ângulo .

Oi pessoal, tudo bem? Vamos analisar essa questão.

A situação exposta no enunciado está descrita na figura abaixo:

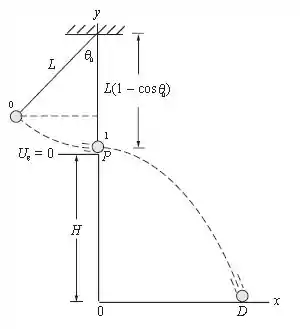
Pelas regras de lançamento horizontal, temos que:

Precisamos então descobrir a velocidade e o tempo para avaliar do que depende

Usando conservação de energia mecânica, temos:

Temos que , logo:

Substituindo as equações temos:

A velocidade no ponto 1, será:

O tempo do movimento é dado a partir da equação da posição para aceleração constante:

Sabemos que:

Portanto:

Logo, vale: