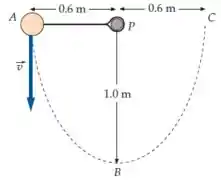
Uma massa pontual de se movendo em uma superfície horizontal sem atrito está preso a uma tira elástica que tem a outra extremidade fixa no ponto . A tira elástica exerce uma força de magnitude , onde é o comprimento da tira e é uma constante desconhecida. A força da tira elástica aponta para . A massa se move ao longo da linha pontilhada na figura abaixo. Quando ela passa pelo ponto , sua velocidade é , com a orientação mostrada; A distância é de e é . (a) Encontre a rapidez da massa nos pontos e . (b) Encontre .

(b) Agora vamos pensar na energia do sistema. Em cada ponto a massa terá certa energia cinética, e certa energia potencial elástica:

Sabemos que a energia deve se conservar nesse sistema, então podemos comparar qualquer par de pontos para encontrar a constante :

Multiplicando tudo por :

E isolando :