Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.2 - Ex. 17

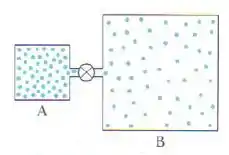
O recipiente A da figura, que contém, um gás ideal à pressão de 5,0.10 5   P a e à temperatura de 300   K , está ligado por um tubo fino (e uma válvula fechada) a um recipiente B cujo volume é quatro vezes maior que o de A . O recipiente B contém o mesmo gás ideal à pressão de 1,0.10 5   P a e à temperatura de 400   K . A válvula é aberta para que as pressões se igualem, mas a temperatura de cada recipiente é mantida. Qual é a nova pressão nos dois recipientes?

Passo 1

Falaa galerinha mais esperta desse Brasil, tudo jóia:

Essa é uma questão perigosa. Pode ser complicado saber por onde começar, mas vamos lá, começamos escrevendo tudo o que a gente sabe:

Ah, daqui em diante a apóstrofe ( ' ) quer dizer “depois que a válvula foi aberta”, beleza?

Usando a lei dos gases ideais para o recipiente A e B antes e depois de abrir a válvula:

p A V A = n A R T A

p B 4 V A = n B R T B

p A ' V A = n A ' R T A

p B ' ( 4 V A ) = n B ' R T B

Veja que as temperaturas e os volumes não mudam, por isso eles não tem apóstrofe.

Passo 2

A informação mais importante que a gente tem é que, depois que as válvulas são abertas, as pressões dos dois recipientes ficam iguais:

p A ' = p B '

Substituindo as equações aqui:

n A ' R T A V A = n B ' R T B ( 4 V A )

n A ' T A = n B ' T B 4

Outra coisa que sabemos é que o número de mols no sistema inteiro não muda, porque ele é fechado. Então:

C o n s t a n t e = N = n A + n B = n A ' + n B '

Então vamos logo isolar os n A e n B iniciais:

n A = p A V A R T A

n B = p B 4 V A R T B

Ou seja:

N = n A + n B = p A V A R T A + 4 p B V A R T B = V A R p A T A + 4 p B T B

Passo 3

Então tá, chegamos em basicamente duas equações:

n A ' T A = n B ' T B 4

V A R p A T A + 4 p B T B = n A ' + n B '

Vamos isolar o n B ' da primeira equação e tentar substituir na segunda:

n B ' = 4 n A ' T A T B

E então a segunda equação fica assim:

V A R p A T A + 4 p B T B = n A ' + 4 n A ' T A T B

V A R p A T A + 4 p B T B = n A ' 1 + 4 T A T B

Agora vamos isolar o n A ' :

n A ' = V A R p A T A + 4 p B T B 1 + 4 T A T B

Beleza, isso já é um resultado interessante.

Passo 4

Agora vamos pegar esse valor de n A ' e substituir na fórmula original:

p A ' V A = n A ' R T A

p A ' V A = V A R p A T A + 4 p B T B 1 + 4 T A T B R T A

Podemos cortar o volume e a constante R :

p A ' = p A T A + 4 p B T B 1 + 4 T A T B T A

E agora é só substituir os valores:

p A ' = 5,0.10 5 300 + 4,0.10 5 400 1 + 1200 400 ( 300 )

p A ' = 5,0.10 5 300 + 4,0.10 5 400 ( 75 )

p A ' = 2,0 × 10 5   P a

Nem foi preciso arredondar, deu exatamente duzentos mil. Um belo resultado.

Enfim, como as duas pressões finais são iguais, a resposta final é essa mesmo:

p f = 2,0 × 10 5   P a

Resposta

A nova pressão é p f = 2,0 × 10 5   P a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18.3. Um tanque cilíndrico possui um pistão bem ajustado que permite alterar o volume do cilindro. O tanque inicialmente contem 0,110m 3 de ar a uma pressão de 3,4 atm. O pistão é lentamente puxado pa
18.9. Um grande tanque cilíndrico contem 0,750m 3 de gás nitrogênio a 27 °C e uma pressão de 1,50 ⋅ 10 5P a (pressão absoluta). O tanque possui um pistão bem ajustado que pode fazer o volume variar. Q
18.1. Um tanque de 20,0L contém 0,225k g de hélio a 18° C . A massa molar do hélio é 4,0g / m o l . A) Quantos moles de hélio existem no tanque? B) Calcule a pressão no tanque em pascals e em atmosfer
18.6. Você tem vários balões idênticos. Empiricamente, você descobre que um balão irá estourar se o volume exceder 0,900 L. A pressão do gás dentro do balão é igual à pressão do ar (1,0 atm). A) Se o
18.7. Um automóvel Jaguar XK8 possui motor com 8 cilindros. No início do tempo da compressão, um dos cilindros contém 499c m 3 de ar sob pressão de uma atmosfera ( 1,01 ⋅ 10 5P a ) e temperatura igual