Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.1 - Ex. 6
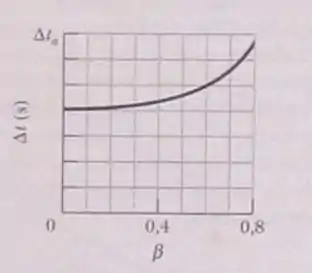
O referencial S’passa pelo referencial S a uma velocidade v ao longo da direção comum dos eixos x’e x, como na figura 37-9. Um observador estacionário no referencial S’mede um certo intervalo de tempo em seu relógio de pulso. Um observador estacionário do referencial S mede o intervalo de tempo correspondendte, . A figura 37-22 mostra a variação de com o parâmetro de velocidade no intervalo . A escala do eixo vertical é definida por . Qual é o valor de para ?
Passo 1
De acordo com a expressão da dilatação do tempo, temos que
Onde .
Dessa forma temos que
Passo 2
De acordo com o gráfico apresentado na questão, temos que para , temos que . Dessa maneira aplicando e
temos
Resposta
O valor aproximado de para é .
Exercícios de Livros Relacionados
A que velocidade um relógio se move se ele funciona a uma taxa de metade da taxa de um relógio em repouso em relação a um observador?
Um relógio atômico move-se a 1000k m / h por 1,00h conforme medido por um relógio idêntico na Terra. Ao final do intervalo de 1,00h , quantos nanossegundos mais lento o relógio em movimento estará em
Um astronauta está viajando em um veículo espacial que se move a 0,500 c em relação à Terra. Ele mede sua frequência cardíaca, cujo valor é 75,0 batidas por minuto. Os sinais gerados pelo seu pulso sã
Uma sonda espacial interestelar é lançada da Terra. Depois de um breve período de aceleração, ela se move a uma velocidade constante, com um módulo de 70,0 % da velocidade da luz. Suas baterias de com
Os gêmeos idênticos Speedo e Goslo se unem para uma migração da Terra para o Planeta X, a 20,0a n o s -luz de um referencial no qual ambos se encontram em repouso. Os gêmeos, de mesma idade, partem no