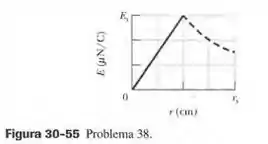
Uma região circular no plano x y é atravessada por um campo magnético uniforme orientado no sentido positivo do eixo z . O módulo B do campo (em teslas) aumenta com o tempo t (em segundos) de acordo com a equação B = a t , em que a é uma constante. A Fig. 30-55 mostra o módulo E do campo elétrico criado por esse aumento do campo magnético em função da distância radial r ; a escala do eixo vertical é definida por E s = 300μ N / C e a escala do eixo horizontal é definida por r s = 4,00c m . Determine o valor de a .

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.6 - Ex. 38

Uma região circular no plano é atravessada por um campo magnético uniforme orientado no sentido positivo do eixo . O módulo do campo (em teslas) aumenta com o tempo (em segundos) de acordo com a equação , em que é uma constante. A Fig. 30-55 mostra o módulo do campo elétrico criado por esse aumento do campo magnético em função da distância radial ; a escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . Determine o valor de .

Passo 1

Essa é uma questão que usa a lei de Faraday na forma integral: a integral de linha do campo elétrica sobre um circuito fechado se relaciona com a variação do fluxo magnético sobre a região limitada por esse circuito:

Pelo gráfico do campo elétrico induzido, vemos que para há uma mudança de comportamento. Dessa forma, somos levados a propor que o campo magnético só existe até esse raio, que denotaremos por :

Passo 2

Consideremos primeiro um circuito fechado circular com raio . Assim, teremos:

Mas por outro lado,

Assim, pela lei de Faraday:

Em módulo,

Passo 3

Note que o resultado obtido no passo anterior representa uma reta no gráfico de contra , que é exatamente o que deve ser! Usando que para , temos , podemos achar :

Assim,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um solenoide longo tem um diâmetro de 12,0c m . Quando o solenoide é percorrido por uma corrente i , um campo magnético uniforme de módulo B = 30,0m T é produzido no interior. Através de uma diminuiçã

A Fig. 30-54 mostra duas regiões circulares, R 1 e R 2 , de raios r 1 = 20,0c m e r 2 = 30,0c m . Em R 1 existe um campo magnético uniforme de módulo B 1 = 50,0m T dirigido para dentro do papel e em R

O campo magnético de um ímã cilíndrico com 3,3c m de diâmetro varia senoidalmente entre 29,6T e 30,0T com uma frequência de 15H z . (Essa variação é produzida pela corrente em um fio enrolado em um ím

Um campo magnético uniforme B → é perpendicular ao plano de uma espira de raio r . O módulo do campo varia com o tempo de acrodo com a equação B = B o e t τ , onde B o e τ são constantes. Escreva uma

A figura 30-70a mostra uma espira retangular de resistência R = 0,020Ω , altura H = 1,5c m e comprimento D = 2,5c m , que é puxada com velocidade escalar constante v = 40c m / s e passa por duas regiõ