Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.6 - Ex. 39

O campo magnético de um ímã cilíndrico com 3,3   c m de diâmetro varia senoidalmente entre 29,6   T e 30,0   T com uma frequência de 15   H z . (Essa variação é produzida pela corrente em um fio enrolado em um ímã permanente.) Qual é a amplitude do campo elétrico induzido por essa variação a uma distância de 1,6   c m do eixo do cilindro?

Passo 1

Fala aí! tudo certinho? 😇

Nesse problema temos um campo magnético de um ímã cilíndrico com 3,3   c m de diâmetro que varia senoidalmente entre 29,6   T e 30,0   T com uma frequência de 15   H z . A partir daí queremos saber qual é a amplitude do campo elétrico induzido por essa variação a uma distância de 1,6   c m do eixo do cilindro.

Tem ideia de como fazemos isso? 🤔

Essa é uma questão que usa a lei de Faraday na forma integral: a integral de linha do campo elétrica sobre um circuito fechado se relaciona com a variação do fluxo magnético sobre a região limitada por esse circuito:

∮ E → ⋅ d s → = - d Φ B d t

Veja só! 😉

Passo 2

Note que 1,6 < 3,3 / 2 , de modo que estamos interessados no campo elétrico induzido dentro do ímã. Vamos denotar o raio do ímã por R = 1,65   c m .

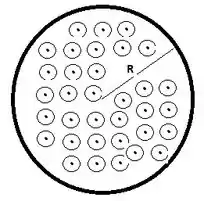
Consideremos um circuito fechado circular com raio r < R . Assim, teremos:

∮ E → ��� d s → = E ⋅ 2 π r

Mas por outro lado,

Φ B = B ⋅ π r 2 ⇒ d Φ B d t = π r 2 d B d t

Assim, pela lei de Faraday:

2 π E r = - π r 2 d B d t ⇒ E = - r 2 d B d t

Tranquilo até aqui? 😉

Passo 3

Precisamos ver agora como B varia no tempo. Sabemos que ele varia senoidalmente entre 29,6   T e 30,0   T , de modo que:

B = B 0 + B a m p   s e n   ( ω t )

Temos que

B 0 = 29,6 + 30,0 2 = 29,8   T

Já B a m p :

B a m p = 30,0 - 29,6 2 = 0,2   T

Assim, temos que

d B d t = ω B a m p cos ⁡ ω t

Assim,

E = - r 2   ω B a m p cos ⁡ ω t

Portanto,

E a m p = r ω B a m p 2

Bacana, não é? 😁

Passo 4

Como f = 15   H z , segue que

ω = 2 π f = 30 π   r a d / s

Portanto, com r = 1,60   c m = 1,60 ⋅ 10 - 2   m e B a m p = 0,2   T , temos que

E a m p = 0,15   V / m

E aí! entendeu tudo? Responde Aí! 😁

Resposta

E a m p = 0,15   V / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29.1. Uma bobina retangular plana com 50 espiras possui dimensões de 25,0 cm por 30,0 cm. Ela está em um campo magnético uniforme, de 12,0 T, com o seu plano no sentido paralelo em relação ao campo. E
29.13. O rotor de um pequeno gerador é constituído por uma bobina chata de seção reta quadrada de lado igual a 1,60 cm, com 120 espiras. A bobina gira em um campo magnético de 0,0750 T. Qual será a ve
29.11. Em uma região do espaço, um campo magnético aponta no sentido positivo de Ox (para direita). Seu módulo varia de posição, de acordo com a fórmula B x = B 0 + b x , em que B 0 e b são constantes
29.2. Em uma experiencia de física feita em um laboratório, uma bobina com 200 espiras, com seção reta de área igual a 12c m 2 , gira em 0,040 s desde uma posição na qual seu plano é perpendicular ao
29.6. Uma bobina com raio de 4,0 cm, com 500 espiras, é colocada em um campo magnético uniforme que varia com o tempo de acordo com a relação B = 0,0120 T s t + 3,0 ⋅ 10 - 5 T s 4 t 4 . A bobina está