Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 9.Problemas - Ex. 71

Uma régua de medição com massa igual a 0,180 kg possui um pivô em uma de suas extremidades, de modo que ela pode girar sem atrito em torno de um eixo horizontal. A régua é mantida em uma posição horizontal e a seguir é liberada. Enquanto ela oscila passando pela vertical, calcule (a) a variação da energia potencial gravitacional ocorrida; (b) a velocidade angular da régua; (c) a velocidade linear na extremidade da régua oposta ao eixo. (d) Compare a resposta da parte (c) com a velocidade de um objeto caindo de uma altura de 1,00 m a partir do repouso.

Passo 1

E aiiiiiiiii galera, tudo bom com vocês?

Vamos fazer mais uma questão!!

Primeiro, fazemos um diagrama para visualizar melhor:

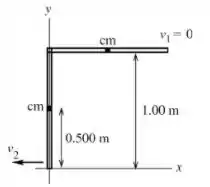
Pegue a origem das coordenadas no ponto mais baixo atingido pela régua e tome +y como a direção positiva para cima.

Passo 2

Letra a:

Use:

U = M g y c m

Δ U = U 2 - U 1 = M g y c m 2 - y c m 1

O centro de massa da régua de medição está em seu centro geométrico, então y c m l = 1.00 m   e   y c m 2 = 0.50 m .

Então,

Δ U = 0.180 k g 9.80 m s 2 0.50 m - 1.00 m = - 0.882 J

Passo 3

Letra b:

Usando conservação de energia:

K 1 + U 1 + W outro   = K 2 + U 2

A gravidade é a única força que atua na régua, então

W outro   = 0 .

K 1 = 0

Então,

K 2 = U 1 - U 2 = - Δ U

Onde Δ U já foi calculado antes

K 2 = 1 2 I ω 2 2   então   1 2 I ω 2 2 = - Δ U e ω 2 = 2 ( - Δ U ) / I

ω 2 = 6 - Δ U M L 2 = 6 0.882 J ( 0.180 k g ) ( 1.00 m ) 2 = 5.42 r a d s

Passo 4

Letra c:

v = r ω = 1.00 m 5.42 r a d s = 5.42 m s

Passo 5

Letra d:

Para uma partícula em queda livre, com y para cima, v 0 , = 0 ;     y - y 0 = - 1.00 m ;             a y = - 9.80 m / s 2 ;   e   v y = ?

v y = - 2 a y y - y 0 = - 2 - 9.80 m s 2 - 1.00 m = - 4.43 m s

Resposta

  1. - 0.882 J
  2. 5.42 r a d s
  3. 5.42 m s
  4. - 4.43 m s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda de uma bicicleta possui velocidade angular de 1,50r a d / s . a) Se sua aceleração angular é constante e igual a 0,300r a d / s 2 , qual é sua velocidade angular para t = 2,50s ?b) Qual foi o d
A lâmina rotatória de um misturador gira com aceleração angular constante igual a 1,50 r a d / s 2 . a) Partindo do repouso, quanto tempo ela leva para atingir uma velocidade angular de 36,0r a d / s
Para t = 0 , a roda de um esmeril possui velocidade angular igual a 24,0r a d / s . Ela possui uma aceleração angular constante igual a 30,0r a d / s 2 quando um freio é acionado em t = 2,0s . A parti
A unidade de disco de um computador é ligada a partir do repouso e possui aceleração angular constante. Se levou 0,750s para a unidade fazer a sua segunda revolução completa, a) quanto tempo ela levou
a) Deduza a E q u a ç ã o( 9.12 ) çã combinando a E q u a ç ã o9.7 çã com a E q u a ç ã o( 9.11 ) çã para eliminar t . b) A velocidade angular da hélice de um avião cresce de 12,0r a d / s até 16,0r a