Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.9 - Ex. 37
Remova o capacitor do circuito da Fig. 31-7 e faça , , e . Determine o valor (a) de ; (b) de ; (c) de . (d) Desenhe um diagrama fasorial.
Passo 1
O problema fala de um circuito em que removemos o capacitor, isto é, façamos . A impedância é dada por
Como , temos que
Mas temos que
Usando e , temos que
Assim, usando , achamos a impedância:
Passo 2
No item (b) nós queremos achar a fase entre a tensão e a corrente, dada por
Como , segue que
Assim, usando os valores que já conhecemos:
Note que, como a fase é positiva, a corrente está atrasada com relação à fem.
Passo 3
Agora devemos achar a amplitude da corrente, dada por
Assim, usando e , obtemos
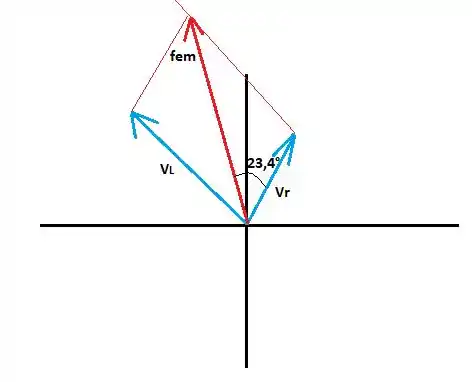
Passo 4
Por fim, precisamos fazer um diagrama de fasores girando no sentido anti-horário. Como vimos, a corrente está atrasada com relação à fem, de modo que a tensão no resistor também estará atrasada com relação à fem. Assim, o diagrama será algo do tipo:
