Um rio de de largura corre com velocidade constante de em uma floresta, na direção leste. Um explorador deseja sair de uma pequena clareira na margem sul e atravessar o rio em um barco a motor que se move com uma velocidade escalar constante de em relação à água. Existe outra clareira na margem norte, rio acima do ponto de vista de um local da margem sul exatamente em frente à segunda clareira. (a) Em que direção o barco deve ser apontado para viajar em linha reta e chegar à clareira da margem norte? (b) Quanto tempo o barco leva para atravessar o rio e chegar à clareira?

Então galera, nesse tipo de problema é sempre importante visualizar o que está acontecendo, para isso, desenhamos a trajetória realizada pelo barco começando na clareira da margem sul, traçando uma reta de de comprimento na direção norte (para cima, na figura):

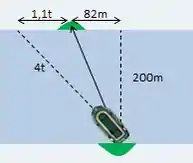
Que atravessa o rio, e uma reta na direção oeste (rio acima, para a esquerda no desenho), ao longo da margem norte do rio, por uma distância dada como:

Na qual o termo que depende de é a distância que o barco irá percorrer paralelamente às margens durante o tempo por causa da correnteza do rio. Dessa forma temos que o desenho formado é um triângulo retângulo.

A hipotenusa desse triângulo retângulo (indicada por uma seta na figura) também depende de e da velocidade do barco (em relação à água) e deve ser igual à “soma” pitagórica dos lados do triângulo:

O que nos leva a uma equação do segundo grau em t:

Resolvendo a equação do segundo grau da forma como já estamos acostumados achamos que:

Até aqui , de boa? Bora continuar que ainda não acabou!