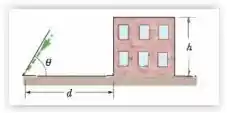
Na Fig. 4 -37, uma bola é lançada para a esquerda da extremidade esquerda do terraço de um edifício. O ponto de lançamento está a uma altura em relação ao solo e a bola chega ao solo depois, a uma distância horizontal do ponto de lançamento e fazendo um ângulo com a horizontal.

(a) Determine o valor de . (Sugestão: uma forma de resolver o problema é inverter o movimento, como se você estivesse vendo um filme de trás para a frente).

Quais são (b) o módulo e (c) o ângulo em relação à horizontal com o qual a bola foi lançada?

Então pessoal , vamos seguir a sugestão e imaginar que a bola foi lançada do solo ao invés do terraço . O movimento como um todo pode ser dividido em movimento uniforme em relação ao eixo e movimento uniformemente variado em relação ao eixo . A primeira coisa que devemos fazer , portanto , é calcular a velocidade inicial em relação aos dois eixos :

Como o movimento na horizontal é uniforme , podemos achar a velocidade com a qual a bola chega ao solo através da relação :

Como o movimento na vertical é uniformemente variado , a altura pode ser obtida através da relação :