Uma rocha de é erguida de uma pedreira com de profundidade, por uma corrente longa e uniforme, com massa de . Essa corrente tem força uniforme, mas em qualquer ponto ela pode suportar uma tensão máxima não superior a vezes o seu peso, sem que se rompa.

a) Qual é a aceleração máxima que a rocha pode atingir para conseguir sair da pedreira e

b) quanto tempo leva para ela ser içada à aceleração máxima, considerando-se que parte do repouso?

Desenhando o diagrama de corpo livre do nosso sistema, temos:

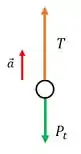
Esse ponto representa a rocha e a corrente como um corpo único. Logo a massa total é o somatório das massas, ou seja:

Ele diz que a tensão na corda não pode exercer vezes o peso da corrente. Como a gente quer a aceleração máxima, vamos achar essa tensão máxima limite que podemos ter fazendo:

Como o peso da corrente é igual a , temos:

E substituindo os dados do enunciado, ficamos com:

Com essas coisinhas calculadas, podemos aplicar a segunda lei de Newton nesse sistema corrente+rocha, considerando para cima para obter:

Como m temos:

Substituindo os valores, ficamos com:

Isolando , encontramos a aceleração:

b) Agora sabendo a aceleração , a velocidade inicial e a distância percorrida pela rocha, podemos usar a equação horária da posição do MRUV e determinar o tempo que a rocha leva para fazer o percurso de subida:

Substituindo , ficamos com:

E substituindo os outros valores, temos:

Valeu, galera! Até a próxima! 😉