Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.4 - Ex. 27

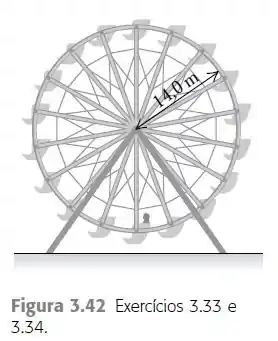
Uma roda-gigante com raio igual a 14,0   m está girando em torno de um eixo horizontal passando pelo seu centro (Figura 3.42). A velocidade linear de uma passageira em sua periferia é igual a 6 , 0   m / s . Determine o módulo, a direção e o sentido da aceleração da passageira a) no ponto mais baixo do movimento circular, b) no ponto mais alto do movimento circular. c)

Quanto tempo leva a roda-gigante para completar uma revolução?

Passo 1

Show de bolinhas pessoal, temos um movimento circular uniforme na roda gigante dada por:

Como temos um movimento circular, temos que a aceleração pode ser dada por:

a r a d = v 2 R

Além disso, temos que:

v = 2 π R T

Bora aplicar!

Passo 2

  1. Temos os seguintes dados: v = 6   m / s R = 14   m , então:

    2. a r a d = 6   m/s 2 14   m

    a r a d = 2,57   m/ s 2

    Com sentido para cima.

    Passo 3

  2. A aceleração radial tem a mesma magnitude que calculamos no item (a), mas agora a direção em direção ao centro do círculo está para baixo. A aceleração neste ponto do movimento é de 2.57 m / s 2 , para baixo.

    3. Passo 4

  3. O tempo para fazer uma rotação é o período T , e a velocidade v   é a distância para uma revolução dividido por T .

Assim:

v = 2 π R T

Então:

T = 2 π R v = 2 π ⋅ 14   m 6.00   m/s

T = 14.7   s

Resposta

  1. a r a d = 2.57   m/ s 2 para cima.
  2. a r a d = - 2.57   m/ s 2 para baixo.
  3. T = 14.7   s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No Ames Research Center, a NASA usa sua grande centrífuga ‘20-G’ para testar os efeitos de acelerações muito grandes (‘hipergravidade’) sobre pilotos e astronautas de teste. Nesse dispositivo, um braç
Em um teste de um ‘aparelho para g’, um voluntário gira em um círculo horizontal de raio igual a 7,0m. Qual é o período da rotação para que a aceleração centrípeta possua módulo de a) 3,0g? b) 10g?
O raio da órbita da Terra em torno do Sol (suposta circular) é igual a 1,50 × 10 8 k m , e a Terra percorre essa órbita em 365d i a s . a) Qual é o módulo da velocidade orbital da Terra em m / s ? b)
Em seu primeiro dia de trabalho em uma fábrica de eletrodomésticos, você é solicitado a informar o que é necessário fazer para que a centrifugadora de uma máquina de lavar triplique sua aceleração cen
Um modelo de rotor de helicóptero possui quatro lâminas, cada qual com 3,40 m de comprimento desde o eixo central até sua extremidade. O modelo gira em um túnel de vento com 550rev/min. a) Qual é a ve