Exercícios de Velocidade e Aceleração Médias no Movimento Circular - Lista de Exercícios Resolvida
Questão 1
Uma partícula descreve um movimento circular de raio , com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor aceleração média é
- ;
- ;
- ;
- ;
- ;
Questão 2
Uma partícula descreve um movimento circular, com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor velocidade média é igual a
Questão 3
Uma formiga pula em uma roda gigante que está descrevendo um movimento circular uniforme de Raio valendo 2m. No instante a velocidade da formiga é , medida em um sistema de coordenadas horizontal. No instante a velocidade é Calcule a aceleração centrípeta e a aceleração média da formiga no intervalo de tempo , que é menor que um período.
Ver solução completaQuestão 4
Um mergulhador realiza giros ao saltar de uma plataforma de metros. Supondo que a velocidade vertical inicial seja nula, determine a velocidade angular média do mergulhador.
Ver solução completaQuestão 5
Considere as seguintes afirmações sobre os vetores velocidade e aceleração de um corpo em movimento:
A velocidade pode ser zero e a aceleração ser diferente de zero.
O módulo do vetor velocidade pode ser constante, com o vetor velocidade mudando com o tempo.
O vetor velocidade pode ser constante mas seu módulo variar com o tempo.
O vetor velocidade pode mudar de sentido com o tempo mesmo que o vetor aceleração permaneça constante.
São verdadeiras as afirmações:
- Todas as afirmações
- I, II e III
- II e III
- I, II e IV
- Nenhuma das afirmações anteriores.
Questão 6
Uma partícula descreve um movimento circular de raio 5m, com velocidade de módulo constante e igual a . Num intervalo de tempo 10 segundos, a partícula anda da circunferência. O módulo de seu vetor velocidade média é igual a
Questão 7
Uma partícula descreve um movimento circular, com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor velocidade média é igual a
Questão 8
Um gato pula em um carrossel que está descrevendo um movimento circular uniforme. No instante a velocidade do gato é , medida em um sistema de coordenadas horizontal. No instante a velocidade é Quais são:
- o módulo da aceleração centrípeta do gato.
- a aceleração média do gato no intervalo de tempo , que é menor que um período.
Questão 9
Uma partícula descreve um movimento circular, com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor velocidade média é igual a
Questão 10
Um bloco de inércia é preso a um bloco de inércia por uma corda que passa por um disco uniforme de inércia e raio que pode rodar em torno do seu eixo. Inicialmente, o bloco de inércia é colocado de tal forma que a corda está tensionada. Ignore o atrito entre o disco e o eixo de rotação.
- Determine a aceleração angular da polia quando o sistema é liberado.
- Se o sistema é liberado a partir do repouso, qual é a velocidade do bloco de inércia após ele ter descido uma altura ?

Questão 11
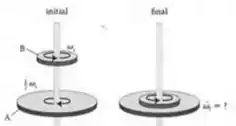
O disco A na figura abaixo, com raio e inércia está inicialmente rodando na direção horária, como visto de cima com uma velocidade angular . O disco , de inércia e raio , está inicialmente rodando na direção anti-horária com velocidade angular . Os dois discos estão restritos a rodar em torno do mesmo eixo, que passa pelo centro de ambos os discos. Há atrito entre os discos, de forma que após entrarem em contato os discos giram com a mesma velocidade angular .
- Qual é a velocidade angular final, , do sistema?
- Determine a variação de energia térmica do sistema composto pelos dois discos.
Questão 12
(Cap 9 – Ex 36) Uma bicicleta tem rodas de de diâmetro. O ciclista acelera a partir do repouso, com aceleração constante, até , em . Qual é a aceleração angular das rodas?
Ver solução completaQuestão 13
Considere a figura abaixo que mostra uma conta que pode se
movimentar livremente, sem atrito, num aro circular de raio R 0,5 m
montado na vertical. O aro gira com velocidade angular constante de
módulo —14,9 rad/s em torno do seu eixo vertical. A conta está em
repouso em relação ao aro na posição indicada na figura, com 9 300.
Calcule a força centrípeta atuando sobre a conta.
Escolha uma:
a. 6,94 N
b. Nenhuma resposta está correta.
c. 8,33 N
d. 2,78 N
e. 5,55 N
f. 1,39 N
g. 4,16 N
h. 9,71 N
Ver solução completaQuestão 14
Um canhão está preso na borda de um carrossel de raio que pode girar sem atrito sobre um eixo vertical fixo que passa pelo seu centro (ver Figura 2). O carrossel e o canhão têm um momento de inércia total em relação a esse eixo. O conjunto encontra-se inicialmente em repouso. O canhão então dispara uma bala de massa com uma velocidade tangencialmente ao carrossel. O conjunto carrossel + canhão passa a girar devido ao disparo.
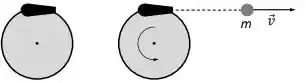
Após o disparo, qual é a velocidade angular do conjunto carrossel + canhão?
Questão 15
Considere uma serra circular movida por um motor. O centro do disco da serra, quando a mesma é usada para cortar madeira, fica submetido a um torque cujo módulo vale . Se, nesta situação, tal disco gira com uma velocidade angular constante de , o trabalho realizado pelo motor em vale:
Questão 16
Uma pessoa de massa está parada na borda de uma plataforma horizontal, de forma circular, com raio e momento de inércia que pode girar livremente em torno de um eixo vertical que passa pelo seu centro. Inicialmente, a plataforma está em repouso em relação ao solo. Num dado instante, a pessoa começa a andar ao longo da borda da plataforma, até atingir a velocidade de módulo em relação ao solo, como mostra a figura. Neste instante, a velocidade angular da plataforma vale:
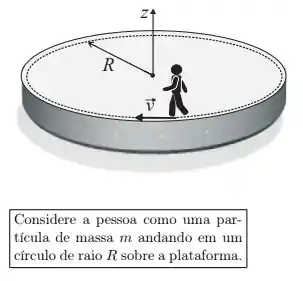
- Zero.
Questão 17
Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:
Com o tempo em segundos.
O módulo da aceleração tangencial da partícula (em ) no instante vale:
Questão 18
Um canhão está preso na borda de um carrossel de raio que pode girar sem atrito sobre um eixo vertical fixo que passa pelo seu centro (ver Figura 2). O carrossel e o canhão têm um momento de inércia total em relação a esse eixo. O conjunto encontra-se inicialmente em repouso. O canhão então dispara uma bala de massa com uma velocidade tangencialmente ao carrossel. O conjunto carrossel + canhão passa a girar devido ao disparo.
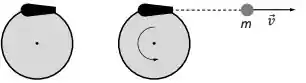
Considere o sistema formado pelo carrossel, canhão e bala. Sejam o momento linear total do sistema, o momento angular total do sistema em relação ao centro do carrossel e a energia mecânica total do sistema. No processo de disparo do canhão, é (são) conservado(s) apenas:
- e
- e
- e
- Nenhum
Questão 19
Uma haste metálica fina, de comprimento e massa , pode girar em torno de um eixo horizontal que a atravessa perpendicularmente (saindo da página), à distância de sua extremidade (ver figura ao lado). A haste é solta a partir do repouso de sua posição horizontal. Calcule:
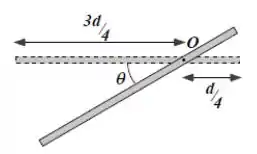
- A velocidade angular e a aceleração angular da haste no instante em que ela faz um ângulo com a horizontal (conforme figura ao lado). Ou seja, calcule e .
Questão 20
Na figura abaixo dois blocos de mesma massa estão ligados por uma corda de massa desprezível, que passa por uma polia em formato de disco com raio e massa . A corda não escorrega na polia, e não há atrito no eixo da polia. Porém, existe atrito cinético entre a mesa e o bloco que escorrega. Quando o sistema é liberado a partir do repouso, a polia gira de em , e a aceleração dos blocos e da polia são constantes.
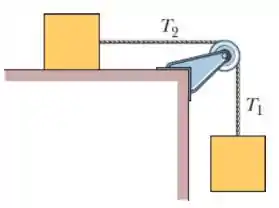
Qual a aceleração dos blocos?
Ver solução completaQuestão 21
Na figura abaixo dois blocos de mesma massa estão ligados por uma corda de massa desprezível, que passa por uma polia em formato de disco com raio e massa . A corda não escorrega na polia, e não há atrito no eixo da polia. Porém, existe atrito cinético entre a mesa e o bloco que escorrega. Quando o sistema é liberado a partir do repouso, a polia gira de em , e a aceleração dos blocos e da polia são constantes.
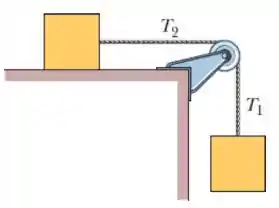
Qual a aceleração angular da polia? Ela é positiva ou negativa?
Ver solução completaQuestão 22
Uma partícula de massa executa um movimento circular, descrito pelo vetor posição
em que , com e constantes positivas.
(c) calcule , o produto vetorial entre os vetores posição e momento linear.
Ver solução completaQuestão 23
(Cap 3 – Ex 69) (a) Quais são o período e a rapidez de uma pessoa em um carrossel, se a pessoa tem uma aceleração com magnitude de 0,80 m/s² quando situada a 4,0 m do eixo? (b) Quais são a magnitude de sua aceleração e sua rapidez, se ela se desloca até uma distância de 2,0 m ao centro do carrossel e o carrossel segue girando com o mesmo período?
Ver solução completaQuestão 24
(Cap 3 – Ex 66) Você está projetando uma centrífuga para girar a uma taxa de . (a) Calcule a máxima aceleração centrípeta que pode suportar um tubo de ensaio preso ao braço da centrífuga a do eixo de rotação. (b) A centrífuga leva e para atingir, a partir do repouso, sua taxa máxima de rotação. Calcule a magnitude da aceleração tangencial da centrífuga, suposta constante, enquanto ela está girando.
Ver solução completaQuestão 25
Um carro de massa está fazendo uma curva circular de raio , que possui inclinação com o chão. Seja o coeficiente de atrito cinético e a magnitude da aceleração da gravidade. Derive uma expressão para um intervalo de velocidade possível necessário para manter o carro movendo no círculo sem derrapar. Expresse suas respostas através das constantes mencionadas no exercício.
Ver solução completaQuestão 26
Um disco de raio e massa gira livremente com velocidade angular em torno de um eixo vertical que passa pelo seu centro de massa. Pela ação de um torque, o eixo de rotação é alterado para a horizontal em um intervalo de tempo , conforme a figura abaixo. Sabendo que o módulo da velocidade angular do disco manteve-se constante durante a aplicação do torque, mostre que o módulo do torque médio aplicado é dado por:
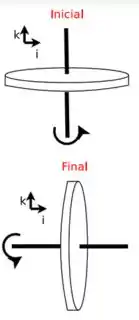
Questão 27
2) Quando se deixa cair uma fatia de pão com manteiga de uma mesa, a fatia adquire um movimento de rotação. Se a distância da mesa ao chão é de e para rotações menores que , determine (a) a menor velocidade angular para qual a fatia cai com a manteiga para baixo.
Ver solução completaQuestão 28
3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos. Em , qual é (a) a posição angular do ponto.
Ver solução completaQuestão 29
3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos.
(c) Qual é a velocidade angular em ?
Ver solução completaQuestão 30
5) Um disco, inicialmente girando a , é freado com uma desaceleração angular constante de módulo . (a) Quanto tempo o disco leva para parar?
Ver solução completaQuestão 31
1) Um mergulhador realiza ao saltar de uma plataforma de . Supondo que a velocidade vertical inicial seja nula, determine a velocidade angular média do mergulhador.
Ver solução completaQuestão 32
2) Quando se deixa cair uma fatia de pão com manteiga de uma mesa, a fatia adquire um movimento de rotação. Se a distância da mesa ao chão é de e para rotações menores que , determine (b) a maior velocidade angular para qual a fatia cai com a manteiga para baixo.
Ver solução completaQuestão 33
3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos. Em , qual é (b) sua velocidade angular?
Ver solução completaQuestão 34
3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos.
(d) calcule a aceleração em ?
Ver solução completaQuestão 35
3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos.
(e) A aceleração angular da roda é constante? Explique.
Ver solução completaQuestão 36
4) A roda da figura tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos. (a) Qual é a menor velocidade que a flecha deve ter?
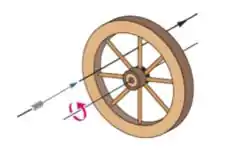
Questão 37
4) A roda da figura tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos. (b) O ponto entre o eixo e a borda da roda por onde a flecha passa faz alguma diferença? Caso a resposta seja afirmativa, para que ponto você deve mirar?
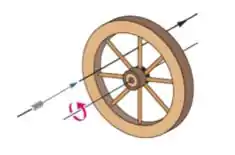
Questão 38
5) Um disco, inicialmente girando a , é freado com uma desaceleração angular constante de módulo . (b) Qual é o deslocamento angular total descrito pelo disco durante esse tempo?
Ver solução completaQuestão 39
6) Um tambor gira em torno de seu eixo central com uma velocidade angular de . Se o tambor é freado a uma taxa constante de , (a) quanto tempo leva para parar?
Ver solução completaQuestão 40
7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em . (a) Qual é o maior ângulo descrito pela reta de referência no sentido positivo?
Ver solução completaQuestão 41
7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em Quais são (b) o primeiro e (c) o segundo instante no qual a reta de referência passa pelo ângulo ?
Ver solução completaQuestão 42
7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em (f) Faça um gráfico de em função de e indique as respostas dos itens (a) a (e) no gráfico.
Ver solução completaQuestão 43
8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (b) o tempo necessário para completar revoluções.
Ver solução completaQuestão 44
8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (d) o número de revoluções desde o repouso até o instante em que o disco atinge a velocidade angular de .
Ver solução completaQuestão 45
11) Na figura abaixo uma roda de raio está acoplada por uma correia a uma roda de raio . A velocidade angular da roda é aumentada a partir do repouso a uma taxa constante de . Determine o tempo necessário para que a roda atinja uma velocidade angular de , supondo que a correia não deslize.
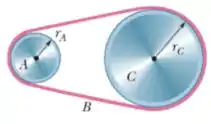
Questão 46
6) Um tambor gira em torno de seu eixo central com uma velocidade angular de . Se o tambor �� freado a uma taxa constante de , (b) Qual é o deslocamento angular total descrito pelo tambor até parar?
Ver solução completaQuestão 47
7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em Quais são (d) instante negativo e (e) instante positivo a reta de referência passa pelo ângulo ?
Ver solução completaQuestão 48
8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (c) o tempo necessário para atingir a velocidade angular de .
Ver solução completaQuestão 49
Uma esfera uniforme de raio e massa gira com velocidade angular inicial em torno do eixo horizontal que passa pelo seu centro, conforme figura ao lado (eixo saindo do papel). Ela é então colocada, no instante , suavemente sobre um piso, cujo coeficiente de atrito cinético com a bola é . Note que no instante inicial em que ela é colocada no piso, ela só possui rotação sem translação (ela está inicialmente só patinando).
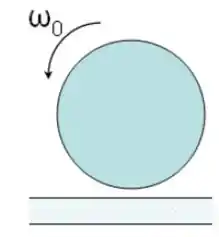
Determine o tempo necessário para ela deixar de patinar, e começar a rolar sem deslizar (rolamento suave).
Quando ela atinge a condição de rolamento suave, qual é a velocidade linear do seu centro de massa e sua velocidade angular de rotação em torno do centro de massa?
Qual a energia térmica produzida entre o instante inicial e o instante em que atinge o rolamento suave?
Ver solução completaQuestão 50
Um cilindro de raio rola sem deslizar com velocidade angular sobre uma correia móvel sob as condições mostradas na figura. No caso (a), a correia move-se com velocidade . No caso (b), a correia move-se com velocidade . Pode-se afirmar que as velocidades do centro do cilindro nos casos (a) e (b) são, respectivamente:
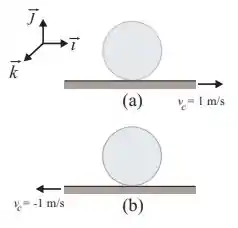
Questão 51
8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (a) a aceleração angular.
Ver solução completaQuestão 52
9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (a) da velocidade angular.
Ver solução completaQuestão 53
9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (b) da velocidade linear
Ver solução completaQuestão 54
9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (c) da aceleração tangencial
Ver solução completaQuestão 55
9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (d) da aceleração radial do astronauta?
Ver solução completaQuestão 56
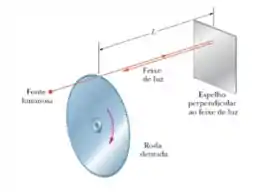
10) Um método para medir a velocidade da luz usa uma roda dentada giratória. Um feixe de luz passa pelo espaço entre dois dentes situados na borda da roda, viaja até um espelho distante e chega de volta à roda exatamente a tempo de passar pelo espaço seguinte entre dois dentes. Uma dessas rodas tem de raio e entre dentes. Medidas realizadas quando o espelho está a uma distância da roda fornecem o valor de para a velocidade da luz. (a) Qual é a velocidade angular (constante) da roda?
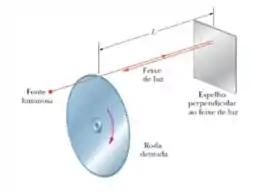
Questão 57
14) Dois cilindros uniformes, ambos girando em torno do eixo central (longitudinal) com uma velocidade angular de , têm a mesma massa de e raios diferentes. Qual é a energia cinética de rotação (b) do cilindro maior, de raio ?
Ver solução completaQuestão 58
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a . O fio passa sem atrito através de um orifício numa placa, e é puxado lentamente para cima até que o ângulo passa a .
Qual foi a variação da velocidade de rotação?
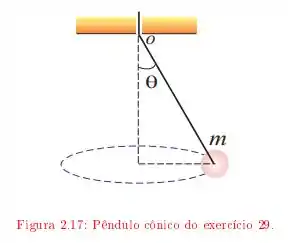
Questão 59
10) Um método para medir a velocidade da luz usa uma roda dentada giratória. Um feixe de luz passa pelo espaço entre dois dentes situados na borda da roda, viaja até um espelho distante e chega de volta à roda exatamente a tempo de passar pelo espaço seguinte entre dois dentes. Uma dessas rodas tem de raio e entre dentes. Medidas realizadas quando o espelho está a uma distância da roda fornecem o valor de para a velocidade da luz. (b) Qual é a velocidade linear de um ponto na borda da roda?
Questão 60
Dois discos homogêneos A e B de massas e raios iguais são fixados por pinos em uma parede vertical, em torno dos quais podem girar sem atrito. Enrola-se em cada um deles um fio ideal em sua periferia, sobre a qual o fio não desliza, e penduram-se blocos de massa iguais a , como mostra a figura.
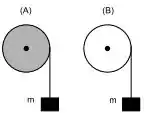
Ao serem os discos A e B libertados a partir do repouso, medem-se, respectivamente, suas acelerações angulares e e os torques sobre eles e , calculados em relação ao centro dos discos. Pode-se relacioná-los corretamente como na opção:
Questão 61
Três cilindros rígidos homogêneos idênticos rolam sem deslizar para a direita sobre uma mesa horizontal. Uma longa placa reta rígida está colocada encima deles e se desloca com velocidade constante módulo como mostrado na figura.
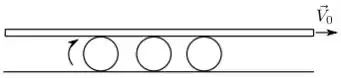
A placa não desliza sobre os cilindros e mantém contato com eles o tempo todo. Podemos afirmar que os cilindros avançam em conjunto com a mesma velocidade de translação de módulo
Questão 62
Um motor é ligado a um disco homogêneo de massa e raio (ver Figura 3). Em algumas situações, uma corda ideal enrolada no disco pode ser conectada a um bloco. A corda não desliza sobre o disco. Considere .
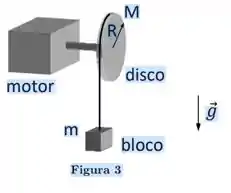
(A) (1,0 ponto) Suponha, inicialmente, a situação em que a corda ainda não esteja conectada ao bloco, ou seja, o bloco ainda não se encontra pendurado na figura ao lado. Nesse caso, a tensão na corda é nula. O motor aplica no disco um torque de módulo , em relação ao seu centro, que o faz girar. Escreva a equação de 2ª lei de Newton para o disco e determine a sua aceleração angular gerada por este torque.
Dado: Momento de inércia de um disco homogêneo de massa e raio em relação a um eixo perpendicular à sua superfície e passando no seu centro: .
(B) (1,5 ponto) Considere, agora, que um bloco de massa foi conectado à corda, como mostra a figura acima. Novamente, o motor aplica um torque , em relação ao centro do disco, que o faz girar, de modo que o bloco sobe verticalmente. Escreva as equações de 2ª lei de Newton para o disco e para o bloco.
(C) (1,5 ponto) Resolva o sistema de equações do item (B) e determine a aceleração angular do disco e a tensão na corda.
Ver solução completaQuestão 63
Um disco horizontal gira com velocidade angular em torno do eixo vertical que passa pelo seu centro. Uma moeda de massa é posta sobre o disco a uma distância do eixo de rotação.
Qual deve ser o coeficiente de atrito mínimo entre a moeda e o disco para que não haja deslizamento?
Questão 64
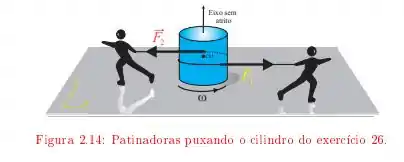
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .
Quantas voltas em torno de seu eixo o cilindro faz durante este tempo?