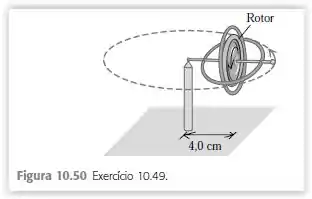
O rotor (volante) de um giroscópio de brinquedo possui massa de . Seu momento de inércia em relação ao seu eixo é igual a . A massa do suporte é de . O giroscópio é suportado em um único pivô () e seu centro de massa está situado a uma distância de do pivô. O giroscópio possui movimento de precessão em um plano horizontal, completando uma revolução em .

a) Ache a força de baixo para cima exercida pelo pivô.

b) Ache a velocidade angular com a qual o rotor gira em torno de seu eixo, expressa em .

c) Faça um diagrama, desenhando vetores para mostrar o momento angular do rotor e o torque que atua sobre ele.

A velocidade angular de precessão escalar é dada pela seguinte expressão:

Onde é a massa, é a aceleração da gravidade, é o raio, é o momento de inércia e é a velocidade angular.

Para resolvermos o problema, precisaremos achar a força de baixo para cima. Assim, podemos relacionar com a segunda lei de Newton

Onde é a força.

O giroscópio tem um rotor e um suporte, isso significa que precisamos da massa total expressa por:

Podemos calcular a velocidade de precessão também pela seguinte relação:

Vamos lá resolver!

Para calcularmos força de cima para baixo, fazemos

Substituindo os dados, temos:

Agora, para o item (b), isolamos a velocidade angular na primeira expressão que colocamos no passo :

Substituindo, temos,

Convertendo as unidades:

Por fim, no item (c), podemos observar o momento angular do rotor e o torque que atua sobre ele pelo seguinte diagrama:

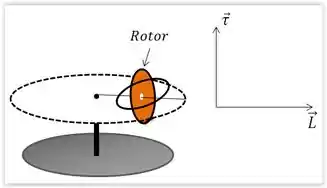
Assim, pela regra da mão direita, a velocidade de precessão e o momento angular atuam da direita para a esquerda, onde a precessão gira no sentido horário, logo, está na direção da precessão e momento angular é ao longo do eixo do rotor.