Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 22

22. Sam ( 75   k g ) sobe uma rampa de neve de 50   m de altura, inclinada em 10 ° , com seus esquis movidos a jato. Os esquis desenvolvem um empuxo de 200   N . Ele mantém seus esquis inclinados em 10 ° depois de iniciar a decolagem, como ilustrado na FIGURA P 8.22 . A que distância horizontal da base do penhasco Sam aterrissará?

Passo 1

Opa! Aqui vamos nós de novo!

Olha só! Primeiramente vamos fazer um desenhozinho pra entender mais ou menos como vai se dar nosso problema...

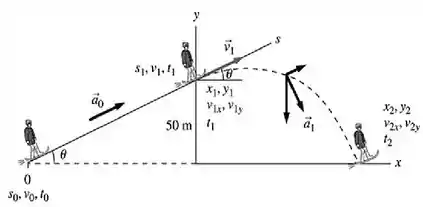
Dessa figura, sabemos que para enquanto o garoto está na rampa...

s 0 = v 0 = t 0 = 0

m = 75   k g

θ = 10 °

s 1 = 50   m sen ⁡ 10 ° = 288   m

E em seguida, quando ele está prestes a sair dela...

x 1 = 0,0   m

y 1 = 50,0   m

t 1 = 0

y 2 = 0

F = 200   N

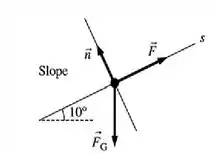
Feito isso, bora partir pro diagrama de de corpo livre do nosso amigo quando ele está na rampa;

E depois, quando ele sai dela, já no ar...

Passo 2

Bom! Terminada essa parte introdutória. Vamos pro que interessa, os cálculos.

Na direção s , ou seja, a direção da rampa, vamos calcular o quanto vai valer a velocidade do garoto quanto está prestes a sair da rampa.

Para isso, apliquemos o somatório das forças em s :

∑ F s = m a 0

F - F G sen ⁡ 10 ° = m a 0

F - m g sen ⁡ 10 ° = m a 0

a 0 = F m - g sen ⁡ 10 °

a 0 = 200   N 75   k g - ( 9,81   m / s ² ) ⋅ sen ⁡ 10 °

a 0 = 0,965   m / s ²

Com essa aceleração, em seguida, vamos usar T o r r i c e l i para ver o quanto vai valer a velocidade v 1 quando S a m está prestes a sair da pista...

v 1 2 = v 0 2 + 2 a 0 ( s 1 - s 0 )

v 1 2 = 0 + 2 ⋅ ( 0,965   m / s ² ) ( 288,0   m - 0,0   m )

v 1 = 2 ( 0,965   m / s ² ) ( 288,0   m )

v 1 = 23,6   m / s

Obtida essa velocidade, vamos decompô-la nas direções horizontal e vertical, sabendo o valor do ângulo de 10 ° ...

v 1 x = v 1 ⋅ cos ⁡ 10 ° = ( 23,6   m / s ) ⋅ cos ⁡ 10 ° = 23,2   m / s

v 1 y = v 1 ⋅ sen ⁡ 10 ° = ( 23,6   m / s ) ⋅ sen ⁡ 10 ° = 4,10   m / s

Passo 3

Tamo indo bem! Bora agora, descobrir o quanto vão valer as acelerações horizontal e vertical do S a m , quando ele sai da rampa.

Para isso, basta novamente usar a segunda Lei de Newton... Não esquecendo do empuxo de 200   N , com um ângulo de 10 ° , hein!?

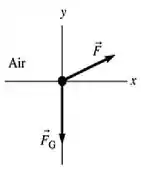
Para a horizontal...

∑ F x = m a x

( 200   N ) ⋅ cos ⁡ 10 ° = ( 75   k g ) a x

a x = ( 200  N ) ⋅ cos ⁡ 10 ° 75   k g

a x = 2,63   m / s ²

Para a vertical...

∑ F y = m a y

200   N ⋅ sen ⁡ 10 ° - 75 ⋅ ( 9,81   m / s ² ) = ( 75   k g ) a y

a y = 200   N ⋅ sen ⁡ 10 ° - 75 ⋅ ( 9,81   m / s ² ) 75   k g

a y = - 9,34   m / s ²

Passo 4

Obtidas essas acelerações, vamos em seguida, pra equação do movimento vertical, que é dado por...

y 2 = y 1 + v 1 y t + 1 2 a y t 2

Sendo que...

A l t u r a   i n i c i a l → y 1 = 50,0   m

A l t u r a   f i n a l → y 2 = 0,0   m

V e l o c i d a d e   i n i c i a l   n a   v e r t i c a l → v 1 y = 4,10   m / s

Logo, nossa equação vai ser...

0,0 = 50   m + ( 4,10   m / s ) t + 1 2 ( - 9,34   m / s ² ) t 2

50   m + ( 4,10   m / s ) t + 1 2 ( - 9,34   m / s ² ) t 2 = 0

Temos então, a seguinte equação do 2 ° grau...

- 4,67 t 2 + 4,10 t + 50 = 0

Cujas raízes são...

t 1,2 = - b ± b 2 - 4 a c 2 a

t 1,2 = - 4,10 ± ( 4,10 ) 2 - 4 ⋅ ( - 4,67 ) ( 50,0 ) 2 ⋅ ( - 4,67 )

t 1,2 = 0,43897 ± - 3,301414   s

Ou seja...

t 1 = 3,74   s

t 2 = - 2,86   s

Como nosso tempo precisa ser positivo, então...

t 1 = 3,74   s

Mas calma que ainda não acabou! Falta apenas um passo, que é calcular a distância horizontal onde S a m   vai parar. Como também temos aceleração em x , bora usar a mesma equação que usamos para y ... Só trocando y por x ;

x 2 = x 1 + v 1 x t + 1 2 a x t 2

E substituindo os valores obtidos...

x 2 = 0,0   m + ( 23,2   m / s ) ( 3,74   s ) + 1 2 ( 2,63   m / s ² ) 3,74   s 2

x 2 = 105   m

Finalmente encontramos a nossa resposta! Essa é a distância horizontal percorrida por S a m quando sai do penhasco!

Resposta

x 2 = 105   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

87. Uri encontra-se em um vôo de Boston, EUA, para Los Angeles. O avião desloca-se a 500 mph em direção 20 ° sudoeste. Val está em um vôo de Miami, EUA, para Seattle. O avião dela está deslocandose a
85. De cima de um trem, um canhão cujo cano forma um ângulo " com a horizontal dispara um projétil para a direita com rapidez v 0 em relação ao trem. O disparo é feito exatamente no momento em que o t
Em qual das situações seguintes o corpo em movimento foi adequadamente modelado como um projétil? Escolha todas as respostas corretas. a) Um sapato é jogado em uma direção arbitrária.b) Um avião a jat
Um astronauta bate numa bola de golfe na Lua. Qual das quantidades seguintes, se houver alguma, permanece constante enquanto a bola percorre o vácuo?a) velocidade escalarb) aceleraçãoc) componente hor
Uma bola de beisebol é lançada do gramado em direção ao apanhador. Quando ela atinge seu ponto mais alto, que afirmação é verdadeira?a) Sua velocidade e aceleração são ambas zero.b) Sua velocidade não