Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 87
87. Uri encontra-se em um vôo de Boston, EUA, para Los Angeles. O avião desloca-se a 500 mph em direção sudoeste. Val está em um vôo de Miami, EUA, para Seattle. O avião dela está deslocandose a para noroeste. Em algum lugar sobre o estado de Kansas, o avião de Uri passa diretamente acima do de Val. Uri está sentado do lado direito e consegue enxergar o avião de Val, abaixo do seu, depois que seu avião passou pelo outro. Uri nota que a fuselagem do avião de Val não está orientada exatamente na direção em que o seu avião se desloca. Qual é o valor do ângulo que a fuselagem forma com a direção do movimento?
Passo 1
Tudo bem senhores!? Aqui vamos nós de novo pra mais uma questãozinha de Cinemática!
E pra resolver esse tipo de questão, já sabe né?
Se liga só! Os aviões são modelados como partículas e estão em movimento relativo, de acordo com as transformações de posição e velocidade.
Designemos o plano de Uri como e a Terra como . se move em relação ao plano com velocidade .
Desse modo, bora fazer um esboço das direções que cada avião está tomando!
Aqui está...
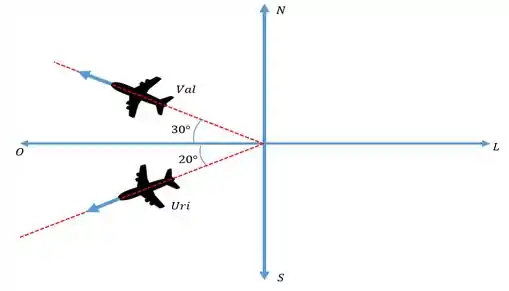
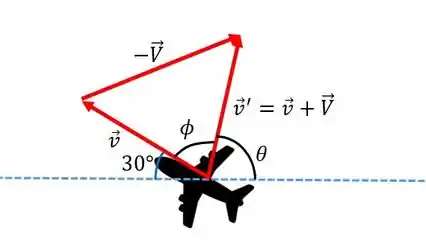
E consequentemente, temos em relação a Uri, no caso o plano ; o seguinte diagrama vetorial de velocidades...
Passo 2
Pela imagem anterior, ao fazer a soma vetorial, podemos ver que...
Onde é a velocidade do avião de Val em relação à terra, é a velocidade do plano de Val em relação ao plano de Uri e é a velocidade do avião de Uri em relação à terra.
Logo, olhando a nossa figura, temos que...
E desse jeito a velocidade vai ser igual à...
Passo 3
Agora ficou moleza! Uma vez que sabemos que...
Então;
Pela figura; podemos ver também que...
Sendo assim, como já conhecemos o valor de :
Foi moleza obter nossa resposta! Esse é o valor do ângulo que a fuselagem forma com a direção do movimento
Pronto! Terminamos aqui!