54. Um pêndulo consiste em uma bola de presa a um fio leve de de comprimento. Quando suspensa em repouso com o fio na vertical, a bola recebe um impulso horizontal, que lhe imprime uma velocidade horizontal de . No instante em que o fio faz um ângulo de com a vertical, qual é:

(a) a rapidez da bola

(b) a energia potencial gravitacional (relativa a seu valor no ponto mais baixo)

(c) a tensão no fio?

(d) Qual o ângulo do fio com a vertical quando a bola atinge sua altura máxima?

a) Vamos aplicar a conservação de energia mecânica para o sistema nos instantes e , onde é a notação de energia cinética, é a notação de energia potencial e é o trabalho da força externa. Então, chegamos a:

Mas como , uma vez que não existem forças externas atuando temos que:

Só que e , nada mais são do que a diferença entre as energias finale e inicial e ). Com isso, obtemos que:

Agora, vamos analisar com calma o nosso problema. Considerando que o que queremos inicialmente é o valor da velocidade quando o fio faz um ângulo de com a vertical, sabemos que apenas energia cinética, graças a velocidade inicial, , esta presente no começo. Já no segundo caso, a bola encontra-se a uma altura do nosso referencial, supostamente com uma velocidade . Logo,, de maneira que obtemos que:

Agora, vamos aplicar as fórmulas relativas a cada energia e conseguimos que:

Mas :

Substituindo os valores numéricos correspondentes, obtemos o valor pretendido do ângulo:

b) Bom! Esse é o mais simples de todos, porque já fizemos questão de obter a fórmula da energia potencial nesse instante, e ela é dado por:

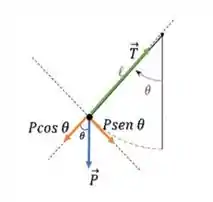
c) Para encontra a tensão agora é preciso ficar atento as forças que agem no nosso problema. Aplicando o somatório das forças na direção radial, temos:

Temos, então da figura, como o bola está sendo girado com o uso de um fio, que há uma tensão agindo sobre ela, igual a . Temos que lembrar também que estamos trabalhando na direção radial, logo, apenas uma componente da força peso age nessa direção:

Só que esse é a velha e conhecida aceleração centrípeta:

Obtemos o valor de lá na letra, e o ângulo , já temos. Agora é só ir pro abraço!

d) Bom essa pergunta que faz a letra d, já estamos até cansados de resolver. Todos sabemos que o único de energia disponível na altura máxima de um pêndulo é a energia potencial gravitacional, que para esse caso chamaremos de . Logo basta igualar à energia cinética lá em , que encontraremos o que desejamos:

Só que =

Façamos as substituições numéricas: