Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 86

Quais são os valores médios e os valores rms da corrente para as duas formas de onda de corrente mostradas na Figura 29-46?

a)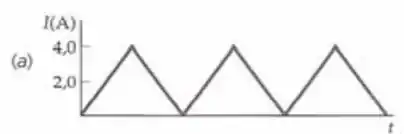

b)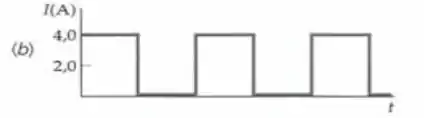

Passo 1

a)

Meus caros!

Da definição, temos que:

I a v = 1 ∆ T ∫ 0 ∆ T I   d t

I r m s = I 2 a v

Notemos que, durante a primeira parte do ciclo:

I a = 4   A ∆ T t

Com isso:

I a v ,       a = 1 ∆ T ∫ 0 ∆ T 4   A ∆ T t   d t = 4   A ∆ T 2 ∫ 0 ∆ T t   d t = 4   A ∆ T 2 t 2 2 ∆ T 0  

I a v ,       a = 2.0   A

Observem:

I a 2 = 4.0   A 2 ∆ T 2 t 2

Refazendo:

I a 2 a v = 1 ∆ T ∫ 0 ∆ T 4   A 2 ∆ T 2 t 2   d t = 4   A 2 ∆ T 3 ∫ 0 ∆ T t 2   d t = 4   A 2 ∆ T 3 t 3 3 ∆ T 0

I a 2 a v = 16 3   A 2

Por fim:

I r m s ,       a = 16 3 A 2

I r m s ,       a = 2.3   A

Passo 2

b)

Da definição, temos que:

I a v = 1 ∆ T ∫ 0 ∆ T I   d t

I r m s = I 2 a v

Notemos que a segunda etapa do ciclo é igual a zero, vamos expressar em função de ∆ T / 2 :

I a = 4   A ∆ T t

Com isso:

I a v ,       b = 1 ∆ T ∫ 0 ∆ T / 2 4   A ∆ T t   d t = 4   A ∆ T 2 ∫ 0 ∆ T / 2 t   d t = 4   A ∆ T 2 t 2 2 ∆ T / 2 0  

I a v ,       b = 2.0   A

Observem:

I b 2 = 4.0   A 2

Refazendo:

I b 2 a v = 1 ∆ T ∫ 0 ∆ T / 2 4.0   A 2   d t = 4   A 2 ∆ T ∫ 0 ∆ T / 2   d t = 4   A 2 ∆ T t ∆ T / 2 0

I b 2 a v = 8   A 2

Por fim:

I r m s ,       b = 8.0   A 2

I r m s ,       b = 2 . 8   A

Resposta

a )   I r m s ,       a = 2.3   A

b )   I r m s ,       b = 2.8   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A largura de linha relativa a meia altura Δ ω d / ω de uma curva de ressonância como as que aparecem na Fig. 31-16 é a largura de linha na metade do valor máximo de I dividida pela frequência angular
Um aparelho de ar condicionado ligado a uma tomada de 120 V rms é equivalente a uma resistência de 12,0 Ω e uma reatância indutiva de 1,30 Ω ligadas em série. Determine (a) a impedância do aparelho e
Uma fonte alternada com uma força eletromotriz de 6,00V e um ângulo de fase de 30 , 0 ∘ é ligada a um circuito RLC série. Quando a diferença de potencial entre os terminais do capacitor atinge o valor
Uma fonte de corrente alternada de frequência variável, um indutor de indutância L e um resistor de resistência R são ligados em série. A Fig. mostra a impedância Z do circuito em função da frequência
Remova o capacitor do circuito da Fig. 31 - 7 e faça R = 200 Ω , L = 230 m H , f d = 60,0H z e E m = 36,0V . Determine o valor (a) de Z; (b) de ϕ ; (c) de I , (d) Desenhe um diagrama fasorial.