Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 62

Um circuito consiste em um gerador ac ideal, um capacitor de 20 μ F e um resistor de 80   Ω , todos conectados em série. A saída do gerador tem uma fem de pico de 20   V e a carcaça do gerador gira a 400   r a d / s . Determine (a)o fator de potência, (b) a corrente rms e (c) a potência média fornecida pelo gerador.

Passo 1

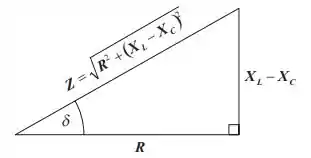
Faala meus queridos, tudo bem com vocês? Espero que sim! Essa questão consiste em achar certos parâmetros para um circuito de um capacitor e um resistor em série. Para facilitarmos nosso entendimento, vou mostrar pra vocês um diagrama com relações entre o fator de potência, as reatâncias e as potências!

Passo 2

Agora galera, vamos usar nada mais nada menos que trigonometria! Isso mesmo, trigonometria! Vem que vou mostrar pra vocês como: no item (a) ele pede o fator de potência. O fator de potência é dado pelo cosseno do ângulo δ . Ou seja:

cos ⁡ δ = R Z = R R 2 + X c 2 = R R 2 + 1 ω 2 C 2

Aplicando os valores numéricos:

cos ⁡ δ = 80   Ω 80   Ω 2 + 1 ( 400 s - 1 ) 2 ( 20 μ F ) 2 = 0.54

E esse é o fator de potência

Passo 3

Agora no item (b) vamos expressar a corrente rms. Essa corrente é a corrente em função da tensão em rms dividida pela impedância do circuito. Vamos pra cima!

I r m s = V r m s Z

Abrindo essa equação, temos:

I r m s = V m a x 2 R 2 + 1 ω 2 C 2

Um monstrinho né?! Mas relaxa, temos todos as variáveis pra isso!

I r m s = 20   V 2 80   Ω 2 + 1 ( 400 s - 1 ) 2 ( 20 μ F ) 2 = 95.3   m A

Passo 4

Belezinha, pra gente finalizar vamos calcular a (c) potência média! Ela é dada pela formula padrão para potência, só que em vez da impedância, vamos usar a resistência do sistema. Fazemos isso para calcular a potência real em cima da resistência que é um valor real:

P m e d i o = I r m s 2 R

P m e d i o = 95.3   m A 2 80   Ω = 0.73   W

E é isso galera, até a próxima!

Resposta

a c o s δ = f p = 0.54

b I r m s = 95.3   m A

c P m e d i o = 0.73   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um circuito L C oscilante, a amplitude da corrente é 7,50 mA, a amplitude da tensão é 250 m V e a capacitância é 220 n F . Determine (a) o período de oscilaçāo; (b) a energia máxima armazenada no c
Em um circuito L C oscilante, L = 3,00 m H e C = 2,70 μ H . No instante t = 0 , a carga do capacitor é zero e a corrente é 2,00 A. (a) Qual é a carga máxima do capacitor? (b) Em que instante de tempo
Um motor elétrico ligado a uma saída de c a de 120V - 60,0H z produz trabalho mecânico na taxa de 0,100h p ( 1h p = 746W ). Sabendo que ele usa uma corrente de 0.650 A (rms), qual é o valor de sua res
Um motor elétrico tem uma resistência efetiva de 32,0Ω e uma reatância indutiva de 45,0Ω quando trabalhando sob carga. A voltagem através da fonte alternada é d c420V ( r m s ) . Calcular o valor médi
Num circuito RLC como o da Fig. 36-2, suponha que R = 5,00Ω ,L = 60,0m H ,f = 60,0H z e ε m = 30,0V Para que valores da capacitância a laxa média de dissipação de energia no resistor seria (a) um máxi