Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 1.Problemas - Ex. 15
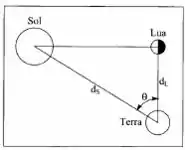
No século III A.C., o astrônomo grego Aristarco de Samos estimou a razão entre a distância da Terra ao Sol e a distância da Terra á lua medindo o ângulo entre as direções em que a Lua e o sol são vistos da terra quando a lua está exatamente “ meio cheia “( metade do disco lunar iluminado: veja a fig.). O valor que obteve foi . a) Encontre a estimativa de Aristarco para b) Com base nos valores atualmente conhecidos . Ache o valor real de e critique o método de Aristarco.
Passo 1
- Pela figura podemos estimar simplesmente calculando o .
- Como
Passo 2
O método de Aristarco foi uma boa ideia, mas essa medida estava sujeita a muitos erros experimentais e pequenas variações no ângulo medido podem alterar absurdamente a razão.
Resposta
Exercícios de Livros Relacionados
Você e um amigo estão caminhando por uma região grande e plana e decidem determinar a altura de um distante pico de montanha, e também a distância horizontal entre vocês e o pico (Figura 1-19). Para i
Algumas estimativas boas sobre o corpo humano podem ser feitas se supusermos que somos feitos majoritariamente de água. A massa de uma molécula de água é 29,9.10 - 27k g . Se a massa de uma pessoa é 6
Em 1989, cientistas da IBM movimentaram átomos com um microscópio de tunelamento com varredura (scanning tunneling microscope, STM). Uma das primeiras imagens vistas pelo público em geral foi a das le
(a) Estime o número de galões de gasolina usados por dia por automóveis nos Estados Unidos, e a quantidade total de dinheiro gasto nela. (b) Se 19,4 galões de gasolina podem ser feitos a partir de um
Um megabyte ( M B ) é uma unidade de armazenamento de memória computacional. Um CD tem capacidade de armazenamento de 700M B e pode armazenar aproximadamente 70m i n de música com alta qualidade. (a)