Uma semente de melancia possui as seguintes coordenadas: . Determine o vetor posição dasemente (a) na notação de vetores unitários e como (b) um módulo e (c) um ângulo em relação ao sentido positivo do eixo (d) Desenhe o vetor em um sistema de coordenadas dextrogiro. Se a semente é transportada para as coordenadas, determine o deslocamento (e) na notação de vetores unitários e como (f) um módulo e (g) um ângulo em relação ao sentido positivo do eixo .
Passo 1
Para responder (a) apenas passamos os eixos para ,respectivamente, , já que não possui valor em . Assim,
Passo 2
O módulo em (b) pode ser calculado a partir do Teorema do Tio Piti (), chegando no resultado de:
Passo 3
Para encontrarmos o ângulo pedido em (c) devemos pensar na função inversa da tangente, pois temos os dois catetos de um triângulo retângulo. Lembrando que a tangente é o cateto oposto dividio pelo adjacente( y sobre x), a resposta fica mais ou menos assim:
**Lembrando que por termos um y positivo e um negativo o ângulo NECESSARIAMENTE se encontra no 3° Quadrante.
Passo 4
Desenhando o vetor no eixo cartesiano obtemos o seguinte desenho:
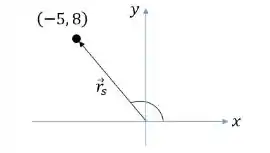
Passo 5
Para calcularmos o deslocamente em (e) precisamos lembrar que o vetor deslocamento é sua variação ( ), isso nos da a seguinte resolução:
Passo 6
O cálculo do módulo em (f) usa o mesmo método do “Passo 2”, repetindo as operações obtemos:
Passo 7
Agora para descobrir o ângulo em (g) também repetimos um método já abordado na resolução, o “Passo 3”. No entanto, os dois catetos possuem valor em módulo de e sua divisão resulta em Lembrando da tabelinha ensinada pela Tia Shirley no 9° ano, sabemos que o ângulo que tem tangente de valor 1 é o , assim, como a coordenada de é negativa, temos o valor de
Resposta
- (b) (c)
(e) (f) (g)