Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.2 - Ex. 3
O vetor posição de um elétron é . (a) Determine o módulo de . (b) Desenhe o vetor em um sistema de coordenadas dextrogiro.
Passo 1
Para determinar o módulo pedido em (a) é muito simples. O vetor nos dá as coordenadas em , se fizermos a raíz da soma dos quadrados delas, obtemos o módulo, isso porque:
Substituindo os valores do enunciado:
Passo 2
(b) Aqui, vamos apenas desenhar nosso vetor:
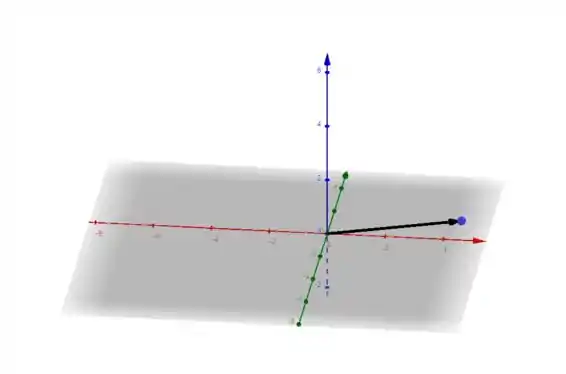
Ele é o carinha em preto ali!
Resposta
(a)
(b) 
Exercícios de Livros Relacionados
Se B → é somado a A → , o resultado é 6 , 0 i ^ + 1 , 0 j ^ . Se B → é subtraído de A → , o resultado é - 4,0 i ^ + 7,0 j ^ . Qual é o módulo de A → ?
Se a → - b → = 2c → , a → + b → = 4 c → e c → = 3 i ^ + 4 j ^ , determine (a) a → e (b) b →
Uma falha geológica é uma ruptura ao longo da qual faces opostas de uma rocha deslizaram uma em relação à outra. Na Fig.3-35, os pontos A e B coincidiam antes de a rocha em primeiro plano deslizar par
Considere dois deslocamentos, um de módulo 3m e outro de módulo 4m . Mostre que os vetores deslocamento podem ser combinados para produzir um deslocamento de módulo (a) 7m , (b) 1m e (c) 5m .
Determine a soma dos quatro vetores a seguir (a) em termos dos vetores unitários e em termos (b) do módulo e (c) do ângulo em relação ao semieixo x positivo. p → = 10,0 m , 25,0 ° s e n t i d o