Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 47
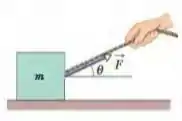
Na Fig. 5-45, um bloco de massa é puxado ao longo de um piso horizontal sem atrito por uma corda que exerce uma força de módulo e ângulo . (a) Qual é o módulo da aceleração do bloco? (b) O módulo da força é aumentado lentamente. Qual é o valor do módulo da força imediatamente antes de o bloco perder contato com o piso? (c) Qual é o módulo da aceleração do bloco na situação do item (b)?
Passo 1
Este trata-se de um problema de aplicação da segunda lei de Newton, por isso precisamos lembrar da fórmula para resolvê-la:
Nesta questão ele nos dá a massa do bloco (), nos diz que o movimento ocorre na horizontal, diz que não há atrito entre o solo e o bloco, nos dá o módulo da força exercida pela corda (), o ângulo que esta força faz com a horizontal () e, a partir, desses dados nos pede o módulo da aceleração do bloco (), além de pedir para analisarmos quando a força é aumentada lentamente qual o módulo da força imediatamente antes do bloco perder o contato com o piso e qual o módulo da aceleração neste caso.
Passo 2
Vamos iniciar esta questão escrevendo a segunda lei de Newton para o eixo , pois é o eixo que ocorre o movimento:
Substituindo os valores conhecidos:
Isolando o :
Nessa nem precisamos usar o eixo , show, né?
Passo 3
Quando começarmos a aumentar a força lentamente e o bloco começar a perder o contato com o chão a normal tenderá a zero, portanto, aplicando a segunda lei de Newton para o eixo :
Como e , então:
Isolando o e substituindo os valores conhecidos:
Passo 4
Com o valor da força em mãos, aplicaremos da mesma maneira que fizemos no passo , na mesma equação, porém com o módulo de diferente. Portanto:
Isolando o e substituindo os valores conhecidos:
Assim, conseguimos determinar o módulo da aceleração direto pelo eixo , pois nos demais eixos a aceleração é nula.
Resposta
- ;
- ;
- .