Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Exercício - Ex. 14
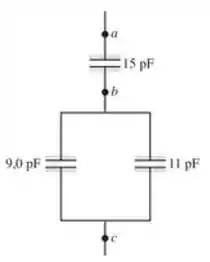
Para o sistema de capacitores mostrado na figura 24.24, ache a capacitância equivalente (a) entre b e c, e (b) entre a e c.
Passo 1
A capacitância equivalente é dada por:
Passo 2
letra a)
Entre os terminais e os capacitores estão em paralelo então:
Passo 3
letra b)
Entre os terminais e tem dois capacitores em paralelo e um capacitor em série com eles.
Primeiro precisamos calcular a capacitância equivalente entre os que estão em paralelo.
Fizemos isso no item anterior e achamos .
Passo 4
Agora precisamos calcular a capacitância equivalente entre e . Como ele estão em série:
Agora calculamos o MMC entre as duas frações:
Resposta
letra a)
letra b)
Exercícios de Livros Relacionados
O capacitor da Fig. 25-25 possui uma capacitância de 25 μF e está inicialmente descarregado. A bateria produz uma diferença de potencial de 120 V. Quando a chave S é fechada, qual é a carga total que
Se um capacitor de placas paralelas inicialmente descarregado, de capacitância C, é ligado a uma bateria, uma das placas, de área A , se torna negativa porque muitos elétrons migram para a superfície.
Pretende-se usar duas placas de metal com 1,00 m 2 de área para construir um capacitor de placas paralelas. (a) Qual deve ser a distância entre as placas para que a capacitância do dispositivo seja 1,
Um capacitar de placas paralelas possui placas circulares com um raio de 8,20 cm, separadas por uma distância de 1,30 mm. (a) Calcule a capacitância. (b) Qual é a carga das placas se uma diferença de
Qual é a capacitância de uma gota formada pela fusão de duas gotas esféricas de mercúrio com 2,00 mm de raio?