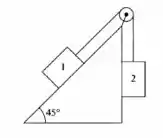
No sistema de figura, o bloco 1 tem massa de 10 Kg e seu coeficiente de atrito estático com o plano inclinado é de 0,5. Entre que valores mínimo e máximo pode variar a massa m do bloco 2 para que o sistema permaneça em equilíbrio.
Passo 1
Galera, o primeiro passo aqui é identificar as situações em que o sistema pode se deslocar, bora lá!
- Caso 1 : Bloco 2 subindo.
- Corpo 1
- Corpo 2
- Caso 2 : Bloco 2 descendo
- Corpo 1
- Corpo 2
Aqui a tendência de movimento do bloco 1 é descer, de modo que a força de atrito estático atua apontando para cima do plano inclinado. Na situação extrema, ou seja, no momento em que bloco irá se movimentar para baixo nosso sistema estará assim
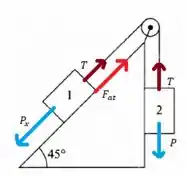
(substituindo na equação do corpo 1)
Sabendo que
Para saber se essa massa é mínima ou a máxima vamos pensar, se a massa 2 diminuisse de valor o corpo 1 escorregaria com mais facilidade, então nossa massa é mínima. Bora pro outro caso!
Passo 2
Aqui a tendência é o bloco 1 subir ao longo do plano, de modo que o atrito tentará impedir isso apontando para baixo, fechou? Fica assim
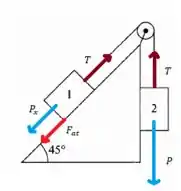
(substituindo na equação do corpo 1)
Essa é nossa massa máxima, já que se aumentasse o corpo 2 desceria e o sistema se movimentaria.