Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 52

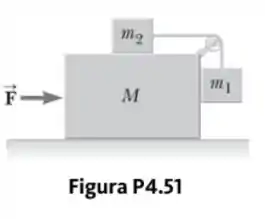
Inicialmente, o sistema dos corpos mostrados na Figura P4.51 é mantido sem movimento. A polia e todas as superfícies não têm atrito. Seja a força   F → zero e assuma que m 1 pode se mover apenas verticalmente. No instante após o sistema dos corpos ter sido liberado, encontre

  1. a tensão T na corda,
  2. a aceleração de m 2 ,
  3. a aceleração de M   e
  4. a aceleração de m 1 .

(Observação: A polia acelera juntamente com o carro.)

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo e bora!

m 1 ( a - A ) = T ⇒ a = T m 1 + A                       ( 1 ) M A = R x = T ⇒ A = T M                 ( 2 ) m 2 a = m 2 g - T ⇒ T = m 2 g - a                 ( 3 )

Passo 2

Letra a:

Substitua o valor por a de [1] por [3] e resolva para T:

T = m 2 g - T m 1 + A

Substitua por A de [2]:

T = m 2 g - T m 1 + T M ⇒ T = m 2 g m 1 M m 1 M + m 2 m 1 + M

Passo 3

Letra b:

Resolva [3] para a e substitua o valor de T:

a = m 2 g m 1 + M m 1 M + m 2 M + m 1

Passo 4

Letra c:

De [2], A = T M . Substitua o valor de T:

A = m 1 m 2 g m 1 M + m 2 m 1 + M

Passo 5

Letra d:

a - A = M m 2 g m 1 M + m 2 m 1 + M

Resposta

  1. T = m 2 g m 1 M m 1 M + m 2 m 1 + M
  2. a = m 2 g m 1 + M m 1 M + m 2 M + m 1
  3. A = m 1 m 2 g m 1 M + m 2 m 1 + M
  4. a - A = M m 2 g m 1 M + m 2 m 1 + M
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A polia de uma máquina de Atwood ideal recebe uma aceleração a para cima, como mostrado na Figura 4-67. Encontre a aceleração de cada massa e a tensão no fio que as liga. Nesta situação, os dois bloco
Em lugar de realizar a experiência da pg. 69 aplicando a força F através de um esforço muscular, podemos aplicá-la ao disco D de massa m através da força-peso de uma massa m’ suspensa da forma indicad
No sistema de figura, o bloco 1 tem massa de 10 Kg e seu coeficiente de atrito estático com o plano inclinado é de 0,5. Entre que valores mínimo e máximo pode variar a massa m do bloco 2 para que o si
No sistema da figura, m 1 = 20K g ,m 2 = 40K gem 3 = 60K g . Desprezando as massas das polias e dos fios e o atrito, calcule a aceleração do sistema e as tensões nos fios 1,2 e 3.
No sistema da figura ( máquina de Atwood) , mostre que a aceleração a da massa M e a tensão T da orda( desprezando as masss da corda e da polia) são dadas por a = M - m M + m g T = 2 m M M + m g