Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 45
Uma criança inventiva chamada Nick quer pegar uma maçã em uma árvore sem escalá-la. Sentado em uma cadeira conectada a uma corda que passa sobre uma polia sem atrito (Fig. P4.45), Nick puxa a ponta solta da corda com uma força tal que a balança de mola lê . O peso real de Nick é e a cadeira pesa . Os pés de Nick não estão tocando o chão.
- Desenhe um par de diagramas mostrando as forças para Nick e a cadeira considerados como sistemas separados, e outro diagrama para Nick e a cadeira considerados como um sistema.
- Mostre que a aceleração do sistema é para cima e encontre seu módulo.
- Encontre a força que o Nick exerce na cadeira.
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
Letra a:
Abaixo, temos os diagramas pedidos:
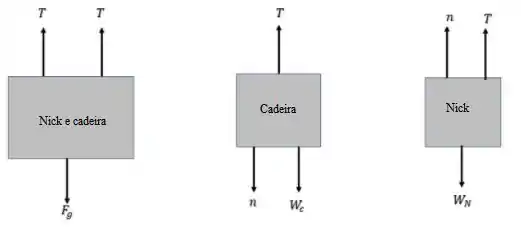
Passo 2
Letra b:
Tomando para cima como a direção positiva, aplicamos a segunda lei de Newton ao sistema de Nick e a cadeira, então obtemos:
Onde é o peso total do sistema e M é a massa total do sistema que são dados por:
Então,
Passo 3
Letra c:
Aplicando a segunda lei de Newton à cadeira:
Onde, :
Resposta
- Ver diagrama
Exercícios de Livros Relacionados
Acelerômetro. A Figura 5.76 mostra um sistema que pode ser usado para medir a sua aceleração. Um observador que caminha sobre a plataforma mede o ângulo θ que o fio que sustenta a bola leve forma com
Um seixo de massa m está sobre o bloco de massa m 2 da máquina de Atwood ideal da Figura 4-60. Encontre a força exercida pelo seixo sobre o bloco de massa m 2 .
As massas penduradas nos dois lados de uma máquina de Atwood ideal consistem em uma pilha de cinco arruelas, cada uma de massa m , como mostrado na Figura 4-65. A tensão no fio é T 0 . Quando uma das
Um bloco de 50k g ésta suspenso de uma corrente uniforme de 1,5m de comprimento que está pendurada do teto. A massa da corrente é 20k g . Determine a tensão na corrente (a) no ponto onde a corrente es
Considere a máquina de Atwood ideal da Figura 4-65. Quando N arruelas são transferidas do lado esquerda para o lado direito, o lado direito desce 47,1c m em 0,40s . Encontre N .