Ache a tensão em cada corda na Figura , sabendo que o peso suspenso é .

Começando pela letra a!

Temos um fio preso por dois pontos fixos em uma mesma horizontal e um peso preso no fio. Abaixo o diagrama de forças:

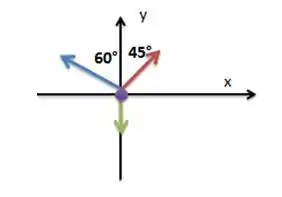
O nó (ponto roxo) que surge das intersecções dos fios é o que estamos analisando nesse diagrama. A força do fio está representada em azul, a do fio em vermelho e do fio em verde. O ângulo com que o fio faz com a vertical é , já o fio é . O sistema está em equilíbrio, então a soma das forças (em cada direção) é zero.

Vamos chamar a tensão do fio de , do fio de e do fio de .

Assim, na direção vertical temos:

E na direção horizontal, temos:

Poxa! Mas aqui temos um sistema com variáveis e apenas duas equações.

Vamos pensar uma coisa! O enunciado nos disse que o peso é suspenso (ou seja: forças em equilíbrio) e que o peso é ! Aha! Aqui está a informação chave!

Olhando apenas para o objeto suspenso temos duas forças agindo sobre ele: a força peso que é vertical para baixo e a força tensora do cabo , que é vertical para cima! Tá, mas e daí? Daí que podemos então determinar a tensão no cabo somando essas forças:

Beleza! Assim nosso sistema que antes tinha três variáveis passa a ter apenas duas! Saca só:

Como , ficamos com:

Assim da segunda equação , e substituindo na primeira:

Usando , temos:

Substituindo os valores de seno e cosseno, teremos:

Racionalizando:

Logo:

E usando a relação para , obtida no passo anterior, ficamos com:

Substituindo na calculadora teremos o valor de :

Para a situação o procedimento é o mesmo. Da mesma forma que no caso anterior, a força de tensão no fio é igual ao peso . Mas temos que ter atenção para os ângulos formados. Segue o diagrama:

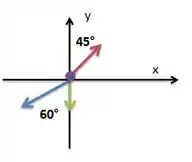
A tensão do fio está em azul e vou chamar de , no fio vou chamar de e está em vermelho e o fio está em verde e a tensão nele é . O ângulo de com a vertical é e de é . Podemos decompor as forças em componentes verticais e horizontais.

Na vertical temos:

Na horizontal:

Temos um sistema com duas equações e duas incógnitas. Da segunda equação podemos isolar :

E substituir na primeira equação:

Usando , temos:

Calculando os valores das funções trigonométricas nos ângulos dados:

Jogando tudo isso na calculadora teremos:

E usando esse valor na expressão para :

Beleza?

Valeu, galera! Até a próxima! 😉