Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 64
Se, no sistema do Problema 64, , , , e o maior ângulo entre a barra e a vertical após a colisão é , determine a rapidez da partícula antes do impacto.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Na figura abaixo, podemos observar o diagrama que representa o sistema depois da colisão:
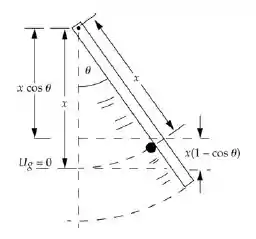
Aplicando a conservação da energia mecânica, temos:
Aplicando conservação de quantidade de movimento angular, temos:
Sabemos que:
Logo:
Substituindo na equação da energia mecância temos:
Simplificando, temos:
Passo 2
Agora é só substituir os valores:
Vamos calcular a parcela do momento de inércia para ficar melhor para visualizar:
Resposta
Exercícios de Livros Relacionados
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Uma bolinha de massa de modelar, de massa m , cai do teto sobre a borda de uma plataforma giratória de raio R e momento de inércia I o que gira livremente com uma rapidez angular ω 0 em torno do seu e
Suponha que, na figura, l = 0,60 m , L = 2,0 m , M = 0,80 k g e m = 0,40 k g . O fio se rompe quando a rapidez angular do sistema se aproxima de um valor crítico ω i , ao mesmo tempo que a tensão no f
Uma barra uniforme, de massa M e comprimento L , está sobre uma mesa horizontal sem atrito. Uma bolinha de massa de modelar, de massa m = M / 4 , move-se ao longo de uma linha perpendicular à barra. D