Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 4.Problemas - Ex. 4
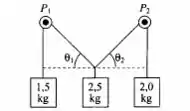
O sistema representado na figura está em equilíbrio. Desprezando as massas dos fios e das polias , calcule os ângulos .
Passo 1
Vamos lá começando com nosso diagrama para entender melhor o problema
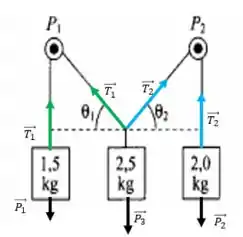
Para que o sistema esteja em equilíbrio primeiramente . Dito isso, ainda as componentes verticais de têm que compensar o peso 3 e as horizontais também se cancelam pra não ter nenhum deslocamento pro lado, show? Bora lá fazer umas continhas legais!
Passo 2
Nossas equações ficam assim
Além disso, temos:
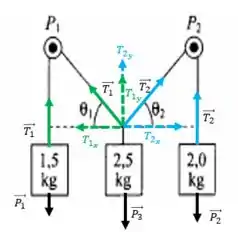
Com isso, temos que trabalhar em cima das componentes das trações também! Como falei anteriormente. Sendo:
No eixo y:
E no eixo x:
Substituindo agora as trações, com os valores que achamos ali em cima, na terceira e quarta equação fica assim ó
Só cortando a gravidade pra ficar bom de visualizar,
Passo 3
Para resolver esse sistema vamos trabalhar com , tranquilo? Então mexendo na equação e elevando ao quadrado todos os lados fica assim
Como nós temos
Mas temos que :
Como no lado esquerdo teremos uma equação com queremos que apareça o seno no lado direto também, então vamos usar a mesma relação praticamente
Vamos desenvolver o lado direito primeiro:
Desenvolvendo o lado esquerdo agora:
Passo 4
Já para basta substituir de volta na equação dos cossenos que tínhamos lá em cima:
Prontinho!