Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 4.Problemas - Ex. 3

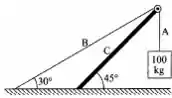
No sistema representado na figura, calcule as tensões nas cordas A e B e a compressão na viga C, desprezando as massas da viga e das cordas.

Passo 1

Para começar nosso probleminha vamos pensar nas forças que atuam sobre os corpos

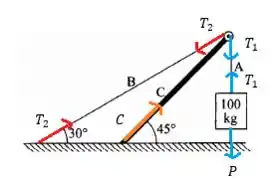
Para que nosso sistema esteja em quilíbrio é preciso haver uma Tensão T 1 que compense o peso no corpo de 100kg, mas essa corda esticada também puxa a viga C, que para não cair pra frente puxa a corda B. Desse modo as tensões T 2   e   T 1 equilibram a viga C empurrando-a pra baixo e criando uma força de compressão C.

Passo 2

Vamos agora começar motando nossas equações de equilíbrio, fechou?

P = T 1

T 1 y + T 2 y = C y

T 2 x = C x

T 1 = 100   .   9,8 = 980   N

  • Notem que T 1   só tem componente vertical, então T 1 = T 1 y

  • Além disso, nossa componente vertical de T 2 se torna T 2 s e n 30 ° = T 2 2 e a horizontal T c o s 30 ° = T 3 2

  • Já C x = C y = C 2 , pois nosso ângulo é de 45 °

Vamos reorganizar nosso sisteminha agora

980 + T 2 2 = C 2

T 2 3 2 = C 2

Show, reorganizando e tirando o C 2 da jogada,

980 + T 2 2 = T 2 3 2

→

980 = T 2 2 3 - 1

→

T 2 = 980   .     2 3 - 1 = 2677   N

Para achar C   basta substituir de volta no nosso sistema, fica assim

C = 980 + T 2 2 2 = 3280   N  

Resposta

T 1 = 980   N

T 2 = 2677   N

C = 3280   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, um cartaz quadrado homogêneo de 50,0k g , de lado L = 2,00 m , está pendurado em uma barra horizontal de comprimento d h = 3,00 m e massa desprezível. Um cabo está preso emm uma extremidade
Na figura, uma barra fina A B de peso desprezível e comprimento L está presa a uma parede vertical poe uma dobradiça no ponto A e é sustentada no ponto B por um fio fino B C que faz um ângulo θ com a
A figura mostra uma viga vertical homogênea de comprimento L que está presa a uma dobradiça na extremidade inferior. Uma força horizontal F a é aplicada à viga a uma distância y da extremidade inferio
A Figura mostra uma viga horizontal homogênea, de massa m b e comprimento L , que é sustentada à esquerda por uma dobradiça presa a uma parede e à direita por um cabo que faz um ângulo θ com a horizon
Na figura, uma esfera de 10k g está presa por um cabo sobre um plano inclinado sem atrito que faz um ângulo θ = 45 ° com a horizontal. O ângulo φ é 25 º º. Calcule a tensão do cabo.