Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.5 - Ex. 52
Um solenoide com de comprimento tem um raio de e uma bobina com espiras: a corrente é . Calcule o módulo do campo magnético no interior do solenoie.
Passo 1
O camp magnético dentro do solenoide é calculado através da lei de Àmpere, traçando uma amperiana retangular como demonstrado na figura abaixo.
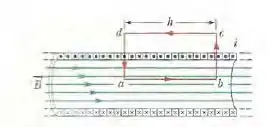
Escrevemos como a soma de quatro integrais, uma para cada segmento da amperiana:
A primeira integral do lado direita é , onde é o módulo do campo uniforme no interior do solenoide e é o comprimento (arbitrário) do segmento . A segunda e a quarta integral são nulas porque, para os elementos desses segmentos, é perpendicular a ou é zero e, portanto, o produto escalar é zero. A terceira integral, que envolve um segmento do lado de fora do solenoide também é nula porque em todos os pontos do lado de fora do solenoide. Assim, o valor de para toda a amperiana é .
Acorrente total envolvida pela amperiana retangular não é igual à corrente nas espiras do solenoide porque as espiras passa mais de uma vez pela amperiana. Seja o número de espiras por unidade de comprimento do solenoide, nesse caso, a amperiana envolve espiras e, portanto,
De acordo com a lei de Àmpere:
Para nossas 1200 espiras, temos:
Resposta
O campo magnético é: