Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 48

Um cabo coaxial consiste em um cilindro condutor sólido que possui um raio igual a 1,00 mm e uma casca cilíndrica condutora que possui um raio interno igual a 2,00 mm e um raio externo igual a 3,00 mm. O cilindro sólido carrega uma corrente de 15,0 A paralela ao eixo central. O invólucro cilíndrico carrega uma corrente de 15,0 A na direção oposta. Suponha que as densidades de corrente estejam uniformemente distribuídas em ambos os condutores. (a) Usando um programa de planilha ou calculadora gráfica, represente graficamente a magnitude do campo magnético como uma função das Fontes do campo magnético, distância radial r do eixo central para 0 3,00 mm?

Passo 1

Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, seja r1 = 1,00 mm, r2 = 2,00 mm e r3 = 3,00 mm e aplique a lei de Ampère em cada uma das três regiões para obter expressões para B em cada parte do cabo coaxial e fora do cabo coaxial. (a) Aplique a lei de Ampère a um caminho circular de raio r

Passo 2

Como a corrente é uniformemente distribuída ao longo da seção transversal do fio interno:

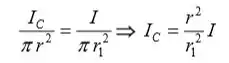
Substitua o IC para obter:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura 27-57 mostra um solenóide que tem n voltas por unidade de comprimento e carrega uma corrente I. Aplique a lei de Ampère à curva retangular mostrada na figura para derivar uma expressão para a

Uma casca cilíndrica longa, reta e de parede fina de raio R carrega uma corrente I paralela ao eixo central da casca. Encontre o campo magnético (incluindo a direção) dentro e fora da concha.

Uma longa casca cilíndrica tem um raio interno ae um raio externo b e carrega uma corrente I paralela ao eixo central. Suponha que dentro do material da casca a densidade da corrente esteja uniformeme

Um toróide firmemente enrolado com 1000 voltas tem raio interno de 1,00 cm, raio externo de 2,00 cm e conduz uma corrente de 1,50 A. O toróide está centrado na origem com os centros das voltas individ

Uma lâmina fina e condutora no plano z=0 conduz corrente na direção -x (Figura 27-58a). A lâmina se estende indefinidamente em todas as dirigées e a corrente está uniformemente distribuída. Para deter