Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 2.Questões Conceituais - Ex. 14
Solte uma bola de borracha ou de tênis de uma altura aproximada de 25 cm e observe atentamente quando ela ricocheteia no piso. Desenhe um gráfico para a posição, um para a velocidade e outro para a aceleração representando o movimento da bola desde o instante em que é solta até ela retornar à altura máxima. Desenhe os gráficos alinhados verticalmente de modo que as escalas dos eixos do tempo fiquem perfeitamente alinhadas entre si. Preste atenção especial no instante em que a bola toca o piso. Trata-se de um intervalo de tempo muito curto, mas não nulo.
Passo 1
Antes de montar o gráfico vamos pensar no que está acontecendo.
A bolinha é solta do repouso de uma altura igual a , tem uma velocidade apontando para baixo, que vai aumentando em modulo porque existe a aceleração da gravidade atuando sobre ela. A bolinha vai caindo e no momento em que a bola toca o chão e é ricocheteada a velocidade muda seu sentido, passando a apontar para cima, mas ela vai diminuindo em módulo até ser anulada porque novamente a aceleração da gravidade age sobre ela, mas agora a velocidade e aceleração estão em sentidos contrários. Nessa ocasião a bola vai subindo até a atingir a altura máxima novamente, na qual a velocidade é nula. Show?
Passo 2
Agora, bora montar os gráficos
Posição:
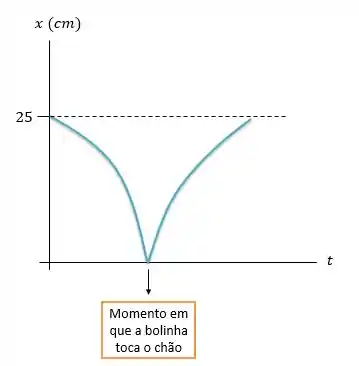
Velocidade:
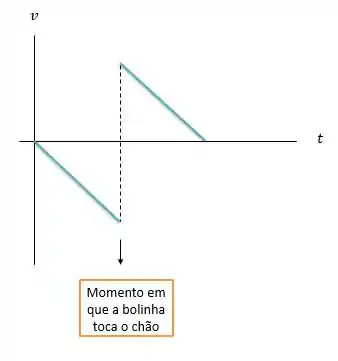
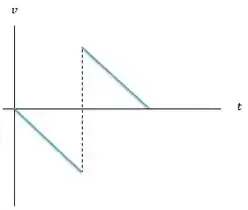
O gráfico de velocidade versus tempo é representado por retas porque a aceleração é constante, sempre igual a aceleração da gravidade. E note que as duas retas, antes de tocar o chão e depois de tocar o chão, são decrescentes e paralelas, mostrando que a aceleração que atua no corpo é sempre a mesma e é negativa, apontando para baixo.
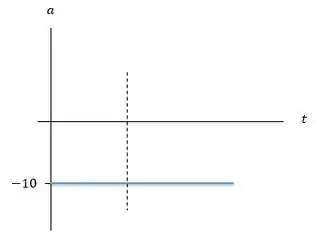
Aceleração:
O gráfico da aceleração é uma reta horizontal em porque a aceleração que age sobre a bolinha é sempre a aceleração da gravidade, que vale aproximadamente e, aponta para baixo.
E é isso !! =)
Resposta
