Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 32
A substancia de trabalho de uma maquina é mol de um gás ideal diatômico. A maquina opera em um ciclo que consiste em três etapas: (1) uma expansão adiabática de um volume inicial de para uma pressão de e um volume de , (2) uma compressão, à pressão constante, até seu volume original de , e (3) aquecimento, a volume constante, até sua pressão original. Determine o rendimento deste ciclo.
Passo 1
A primeira coisa que a gente tem que pensar é em montar o gráfico , mesmo que seja só um esboço. Olha aqui como ele vai ficar!
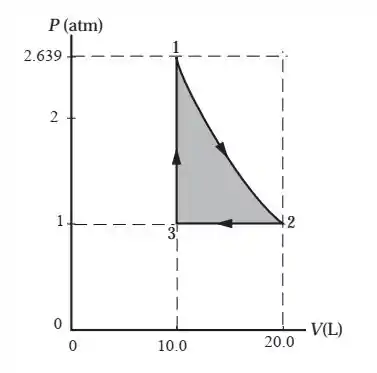
Passo 2
Agora vamos lá! A gente sabe que na transformação adiabática, relacionamos pressão e volume por essa equação aqui:
Então, comparando os dois estados, sabendo que o gás é diatômico:
Passo 3
Vamos calcular o calor trocado em cada etapa:
Processo : adiabática:
Processo : isobárica:
Lá pela equação de Clapeyron, a gente sabe que .
Processo : isovolumétrica:
Lá pela equação de Clapeyron, a gente sabe que .
Então o calor no ciclo é a soma do calor de cada um dos processos:
Passo 4
Agora a gente aplica a primeira lei da termodinâmica pro ciclo todo. O ciclo vai e volta pro mesmo ponto, então a variação de energia interna é nula!
Esse é o trabalho realizado sobre o gás, então o trabalho que o gás realiza é o oposto disso!
O rendimento é igual ao trabalho sobre os calores quentes. Então, substituindo: