Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 22.Exercícios - Ex. 5

5 . Uma superfície hemisférica com raio r , em uma região de campo elétrico uniforme, possui eixo alinhado paralelamente ao sentido do campo. Calcule o fluxo através dessa superfície.

Passo 1

Vem comigo para a gente resolver essa juntos!

A superfície hemisférica que o enunciado quer saber o fluxo através, é o mesmo que metade de uma casa esférica.

O fato do eixo dessa casca está alinha com o campo é mostrado na imagem abaixo:

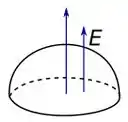
Olhando essa imagem a gente pode ver que a quantidade de campo elétrico que passa pela casca é a mesma quantidade que passa pelo círculo de raio r delimitado pela parte inferior da casca.

Então é a superfície delimitada por esse círculo que vamos usar para o cálculo do fluxo.

Passo 2

A equação do fluxo do campo elétrico é da seguinte forma:

Φ E = ∫ E → ⋅ d A →

Mas como E → e d A → são paralelos nesse caso, temos que:

E → ⋅ d A → = E d A

Então o fluxo fica assim:

Φ E = ∫ E → ⋅ d A → = ∫ E d A

Como o é homogêneo por todo o espeço, temos que:

Φ E = E ∫ d A

Passo 3

A integral do elemento de área d A que chegamos no passo 2 , nada mais é do que a área do círculo, logo:

∫ d A = π r 2

Então temos que o fluxo do campo do na casca esférica é:

Φ E = E π r 2

Questão finalizada com sucesso!

Resposta

Φ E = E π r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.9E Duas partículas de mesma carga q estão separadas por uma distância fixa. Queremos introduzir uma terceira partícula carregada ao conjunto, deforma que todas as partículas sintam força resultante
15.2E Considere um elétron orbitando em torno de um próton, em uma órbita de raio igual a 0,051nm . Calcule a força de atração elétrica entre essas partículas e compare o resultado com a força de atra
15.5E As três esferas vistas na Figura 15.14 têm diâmetro muito menor do que as distancias entre elas. Calcule a relação x / L para que a força sobre a esfera azul seja nula.
15.6E As três esferas vistas na Figura 15.15 têm diâmetro muito menor do que as distancias entre elas. Calcule a relação x / L para que a força sobre a esfera azul seja nula.
15.7E Duas esferas metálicas de mesmo raio a estão separadas uma da outra por distância r muito maior do que a . Uma esfera tem carga q 1 e a outra carga - q 2 , e elas se atraem com força de intensid