Uma superfície plana quadrada com lado igual a é descrita pelas equações
![]()
Faça um desenho do quadrado e mostre os eixo e .
Calcule o fluxo elétrico através do quadrado produzido por uma carga puntiforme positiva localizada na origem . (Sugestão: Imagine o quadrado como parte de um cubo centralizado na origem.)
Passo 1
Visto que o valor de é constante, isso significa que o quadrado possui lados de tamanho determinado pelos intervalos dos eixos e e tem seu vértice no ponto Logo, seu esboço será:
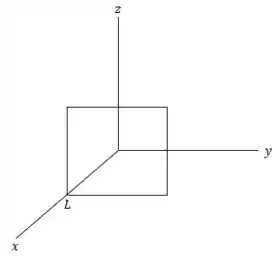
Passo 2
Sabendo que o fluxo elétrico é dado pela lei de Gauss:
Então, visto que se considerarmos apenas o quadrado em questão, o vetor do campo elétrico gerado pela carga situada na origem terá uma angulação que não será fácil de determinar para o cálculo. Assim, para termos o ângulo , podemos considerar que o quadrado é apenas um quarto da face de um quadrado maior de lados , cujo centro está sobre o eixo . Tal quadrado seria uma das faces de uma superfície gaussiana cúbica centrado na origem com arestas .
Passo 3
Dessa forma, o fluxo elétrico sobre a face desse cubo maior será dado por:
E, considerando que a carga esteja uniformemente distribuída por toda a superfície do cubo, o quadrado faz parte de de todas as faces do cubo. Portanto, o seu fluxo elétrico representa do fluxo total: